符号関数 (sign function)

式(1)の符号関数のグラフ
実数 に対して
--- (1)
のように定義される関数 を符号関数 (sign function, or signum function) という.上式は を用いて以下のようにも表せる.
--- (2)
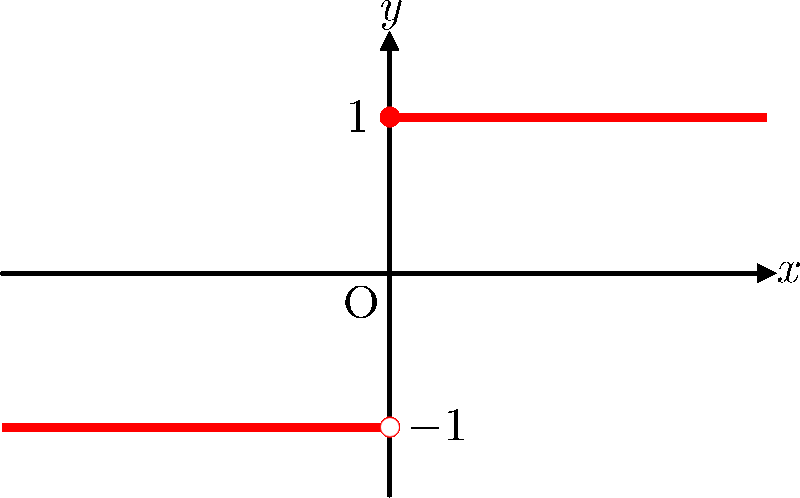
式(3)の符号関数のグラフ
便宜上,次式のように定義される場合もある.
--- (3)
式(3)は以下のようにも表せる.
--- (4)
ヘヴィサイドの階段関数 ( は のときの関数の値 )を用いて表すと
式(1) ⇒
--- (5)
式(3) ⇒
--- (6)
となる.
<置換に対する符号>
線形代数における行列式の定義などで出てくる置換 (permutation) に対して符号関数が用いられることがあり,その場合,置換 が偶置換 (even permutation)か奇置換 (odd permutation) かによって,符号関数 は以下のように定義される:
--- (7)