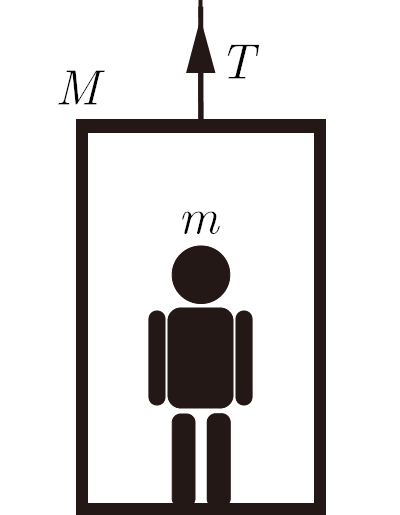エレベーターの運動
図のように,質量
の人が,静止した質量
のエレベータの中に立っていた.時刻
からこのエレベータはロープから鉛直上向きで大きさ
の張力を受けて,時刻
まで鉛直上向きに等加速度直線運動をした.時刻
からエレベータは時刻
での速度のまま 等速直線運動をはじめた.ここで,重力加速度の大きさを
とし,空気抵抗は無視できるものとする.
時刻
から時刻
までのエレベータの加速度の大きさを求めよ.
解答
解説
加速度の鉛直方向成分を
として,鉛直上向きを加速度の正の向きとする.エレベータと人が一体となった物体を考えると,この物体の質量は
であり,この物体にはたらく力は鉛直上向きの張力(大きさ
)と鉛直下向きの重力(大きさ
)の合力である.よって,合力の鉛直方向成分は
と書けて,この物体の運動方程式は
と表せる.したがって,
と求まる.このとき加速度は鉛直上向きであるので,
であり,加速度の大きさは
となる.
閉じる
時刻
から時刻
まで,エレベータが人に作用する垂直抗力(エレベータの床が人を鉛直上向きに押す力)の大きさを求めよ.
解答
解説
垂直抗力の大きさを
として,人に対して運動方程式を立てると
であり,(1)の結果を代入すると
と求まる.
閉じる
解答
閉じる
解説
時刻
での速度を
とおくと,位置,速度,加速度の関係より,時刻
での速度は
と求まる.
閉じる
時刻
以降においてエレベータが等速直線運動をしているとき,張力の大きさ
を求めよ.
解答
解説
等速直線運動をしているということは,加速度が0であるということである.
よって(1)で求めた加速度の式を用いると,
より,
となる.
閉じる
ホーム>>物理演習問題>>力学>>運動>>運動の法則>>エレベーター
学生スタッフ作成
最終更新日2025年7月29日