円筒の慣性モーメント2

図1

円筒の面密度を ${\displaystyle \sigma }$ とすると

${\displaystyle \sigma =\frac{M}{2\pi RL}}$

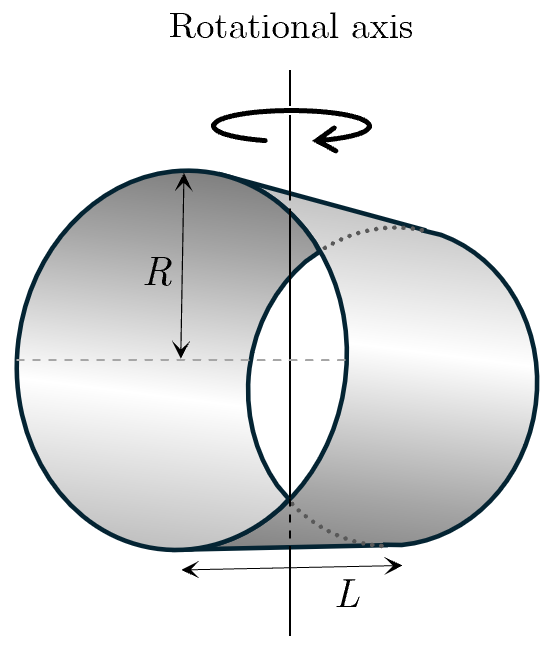
である．図1のように回転軸を ${\displaystyle y}$ 軸にとり， ${\displaystyle y}$ 軸と直交する ${\displaystyle zx}$ 平面をとる．この円筒を ${\displaystyle z}$ 軸方向に微小幅 ${\displaystyle dz}$ でスライスし，多数の円環に分割する．

図2

さらに，円柱座標を考えて，${\displaystyle xy}$ 面上の座標を ${\displaystyle (r,\theta )}$ で表し，図2のように円環の円周を ${\displaystyle \theta }$ 方向で細分化する．このとき，微小円弧の長さ ${\displaystyle dl}$ は

${\displaystyle dl=Rd\theta }$

と表せるので，${\displaystyle z}$ 方向の厚さ ${\displaystyle dz}$ の微小部分の面積 ${\displaystyle dS}$ は

${\displaystyle dS=dl\cdot dz}$ ${\displaystyle =Rd\theta dz}$

である．よって，この微小部分の質量 ${\displaystyle dm}$ は

${\displaystyle dm=\sigma \cdot dS}$ ${\displaystyle =\frac{M}{2\pi RL}\cdot Rd\theta dz}$ ${\displaystyle =\frac{M}{2\pi L}d\theta dz}$

となる．

図3   ${\displaystyle y}$ 軸の先から円筒を見た図

図3から分かるように，この微小部分の回転軸までの距離（回転半径）は ${\displaystyle r=\sqrt{{(R\text{cos}\theta )}^2+z^2}}$ であるので，微小部分の回転軸周りの慣性モーメント ${\displaystyle dI}$ は

${\displaystyle dI=r^{2}dm}$
${\displaystyle \phantom{dI}=(R^2{\text{cos}}^2\theta +z^2)\cdot \frac{M}{2\pi L}d\theta dz}$

と表せる．したがって，求める慣性モーメント ${\displaystyle I}$ は

と求まる．

★ 平行軸の定理を用いて計算

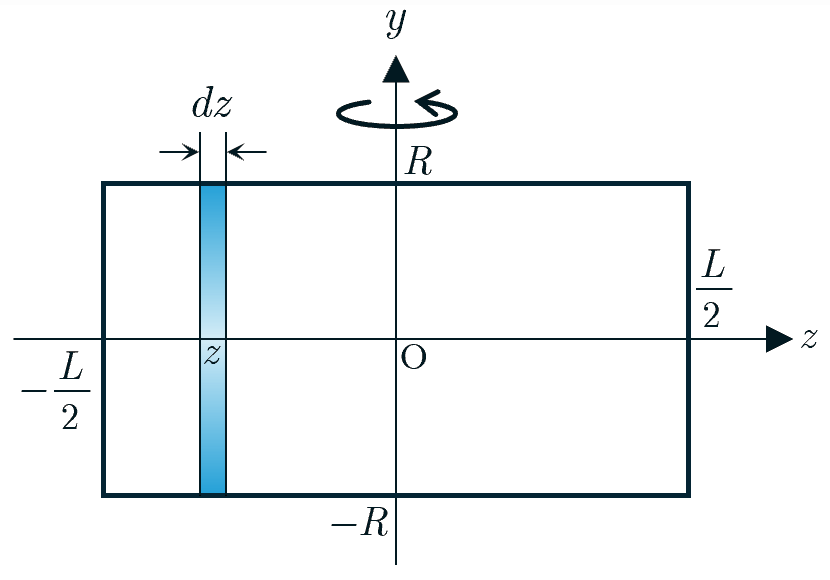図1

円筒の面密度を ${\displaystyle \sigma }$ とすると

${\displaystyle \sigma =\frac{M}{2\pi RL}}$

である．図1のように回転軸を ${\displaystyle y}$ 軸にとり， ${\displaystyle y}$ 軸と直交する ${\displaystyle zx}$ 平面をとる．この円筒を ${\displaystyle z}$ 軸方向に微小幅 ${\displaystyle dz}$ でスライスし，多数の円環に分割すると，1つの円環の微小質量 ${\displaystyle dm}$ は

${\displaystyle dm=\sigma \cdot 2\pi Rdz}$ ${\displaystyle =\frac{M}{L}dz}$

である．位置 ${\displaystyle z=0}$ にある円環の ${\displaystyle y}$ 軸のまわりの慣性モーメント ${\displaystyle d{I}_G}$ は，円環の慣性モーメント2より

${\displaystyle d{I}_G=\frac{1}{2}dm{R}^2}$ ${\displaystyle =\frac{M{R}^2}{2L}dz}$

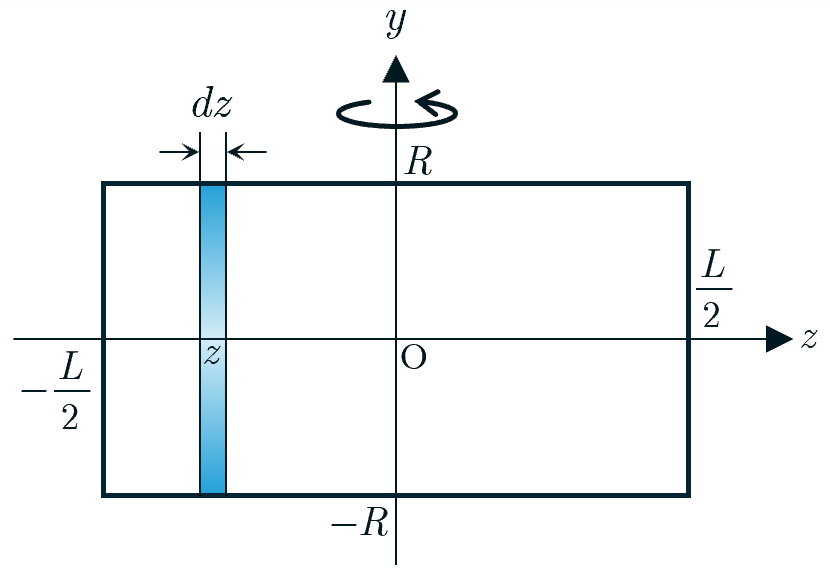図2

である．原点 ${\displaystyle \text{O}}$ から ${\displaystyle z}$ 軸方向に ${\displaystyle z}$ だけ移動した厚さ ${\displaystyle dz}$ の円環（図2）の慣性モーメント ${\displaystyle d{I}_z}$ は，平行軸の定理により

${\displaystyle d{I}_z=d{I}_G+\frac{M}{L}dz\cdot {\left|z\right|}^2}$ ${\displaystyle =\frac{M{R}^2}{2L}dz+\frac{M}{L}{z}^{2}dz}$

であるので，求める慣性モーメント ${\displaystyle I}$ は，

${\displaystyle I={\displaystyle {\int }_{z}d{I}_z}}$ ${\displaystyle ={\displaystyle {\int }_{-\frac{L}{2}}^{\frac{L}{2}}\left(\frac{M{R}^2}{2L}+\frac{M}{L}{z}^2\right)dz}}$ ${\displaystyle ={\left[\frac{M{R}^2}{2L}z+\frac{M}{3L}{z}^3\right]}_{-\frac{L}{2}}^{\frac{L}{2}}}$ ${\displaystyle =\frac{M{R}^2}{2}+\frac{M{L}^2}{12}}$

となる．