慣性モーメント (moment of inertia)

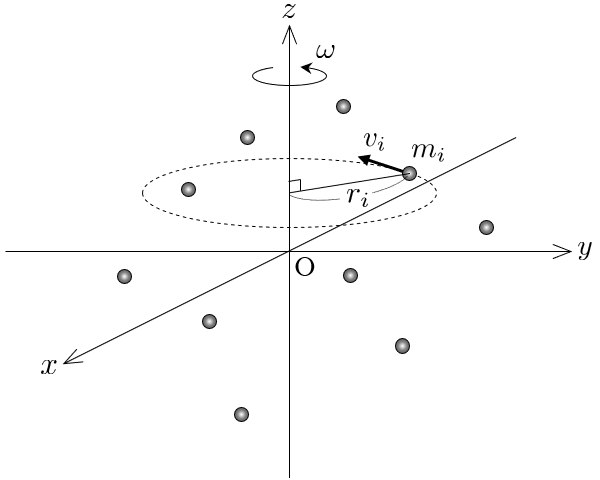
右上図に示すような n 個の質点から成る質点系を考え，この質点系が z 軸のまわりにすべて同じ角速度 ω で回転しているとする．このとき，各質点の質量 mi と z 軸からの距離 ri （回転半径）を用いて表される次の量

I= ∑ i=1 n mi ri2     ---- (1)

を，この質点系の z 軸まわりの慣性モーメントという．慣性モーメント I を用いると質点系の回転運動の方程式は

I dω dt =N     ---- (2)

と表すことができる．ここで， N は質点に作用する z 軸まわりの力のモーメントの和である．したがって，慣性モーメントは，物体が回転運動する際，その回転速度（角速度）の変化を妨げる役割を果たし，物体の回転させにくさを表す量といえる（より正確には物体の回転状態の変化のさせにくさを表す量）．
※ 慣性モーメントの値は，回転軸の取り方によって変わることに注意．

物体の並進運動と回転運動との対応関係を考えると，回転運動における慣性モーメント I の役割は，並進運動において質量が果たす役割に対応している．

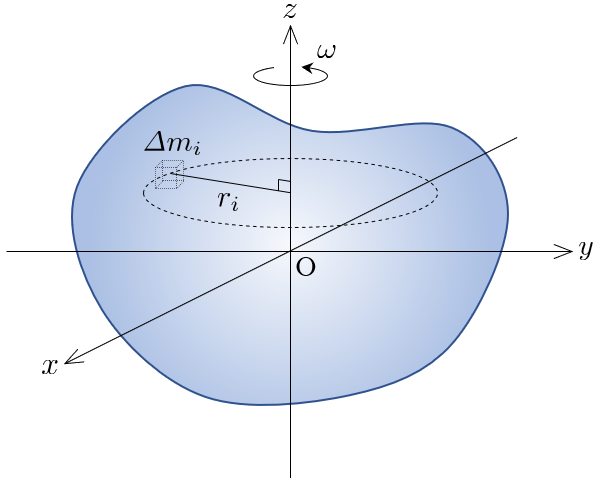
質点系が大きさをもつ連続体である剛体の場合， 剛体を多数の微小部分に細分化し，各微小部分の質量 Δmi と回転半径 ri を式(1)に当てはめて，極限 Δ mi →0 をとると，回転軸まわりの慣性モーメントは

I= lim Δ mi →0 ∑ i=1 n ri2 Δ mi = ∫M r2dm   ---- (3)

のように剛体の全質量 M にわたる積分として表される．剛体の密度を ρ (r) とすると，微小質量 dm は微小体積 dV を用いて dm=ρ (r) dV と書けるので，式(3)は

I= ∫V ρ (r) r2 dV

と表せる．ここで，剛体の密度が一様であれば（全体積 V にわたって一定の値をもつ，つまり ρ (r) =ρ= 定数 ），

I=ρ ∫V r2 dV

と書ける．

計算する際の解法の戦略はこちら

ホーム>>カテゴリー分類>>力学>>剛体の力学>>慣性モーメント