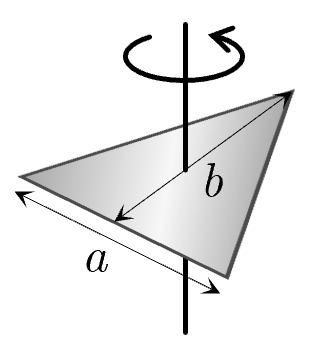
二等辺三角形の薄板の慣性モーメント3

図に示すような，質量 $M$ で密度の一様な二等辺三角形（底辺 $a$ ，高さ $b$ ）の薄板について，薄板の面と垂直で質量中心を通る回転軸のまわりの慣性モーメント $I$ を求めよ．

解答

$I = \frac{M}{6} (\frac{a^{2}}{4} + \frac{b^{2}}{3})$

閉じる

解説（タブを選択して2つの解説を切り替えることができる）

解説1

二等辺三角形の薄板の面密度を $σ$ とすると，この薄板の面積は $S = a b / 2$ なので

$σ = \frac{2 M}{a b}$

である．図のように座標軸を設定し， $x y$ 平面に置かれた二等辺三角形の薄板を $x$ 軸方向と $y$ 軸方向で多数の微小部分に分割する．微小部分の面積は $d S = d x d y$ なので，この部分の微小質量が

$d m = σ \cdot d S$ $= \frac{2 M}{a b} d x d y$

となる．この微小部分の回転半径は $r = \sqrt{x^{2} + y^{2}}$ であるので，回転軸周りの微小慣性モーメントは

$d I = r^{2} d m$ $= \frac{2 M}{a b} (x^{2} + y^{2}) d x d y$

と表せる．図に示すように，二等辺三角形の斜辺の直線の式は

$y = \frac{2 b}{a} x + \frac{2 b}{3}$ $(x < 0)$
$y = - \frac{2 b}{a} x + \frac{2 b}{3}$ $(x \geq 0)$

であり，これを踏まえて積分範囲を設定すると，求める慣性モーメントは

$I = \int_{D} d I$
$= \frac{2 M}{a b} {\int_{- a / 2}^{0} (\int_{- b / 3}^{(2 b / a) x + 2 b / 3} (x^{2} + y^{2}) d y) d x + \int_{0}^{a / 2} (\int_{- b / 3}^{- (2 b / a) x + 2 b / 3} (x^{2} + y^{2}) d y) d x}$
$= \frac{2 M}{a b} {\int_{- a / 2}^{0} {[x^{2} y + \frac{1}{3} y^{3}]}_{- b / 3}^{(2 b / a) x + 2 b / 3} d x + \int_{0}^{a / 2} {[x^{2} y + \frac{1}{3} y^{3}]}_{- b / 3}^{- (2 b / a) x + 2 b / 3} d x}$
$= \frac{2 M}{a b} \int_{- a / 2}^{0} {x^{2} (\frac{2 b}{a} x + b) + \frac{1}{3} ({(\frac{2 b}{a} x + \frac{2 b}{3})}^{3} - {(- \frac{b}{3})}^{3})}$
$+ \frac{2 M}{a b} \int_{0}^{a / 2} {x^{2} (- \frac{2 b}{a} x + b) + \frac{1}{3} ({(- \frac{2 b}{a} x + \frac{2 b}{3})}^{3} - {(- \frac{b}{3})}^{3})}$
$= \frac{2 M}{a b} {[\frac{b}{2 a} x^{4} + \frac{b}{3} x^{3} + \frac{1}{3} {\frac{1}{4} \cdot \frac{a}{2 b} {(\frac{2 b}{a} x + \frac{2 b}{3})}^{4} + {(\frac{b}{3})}^{3} x}]}_{- a / 2}^{0}$
$+ \frac{2 M}{a b} {[- \frac{b}{2 a} x^{4} + \frac{b}{3} x^{3} + \frac{1}{3} {\frac{1}{4} \cdot (- \frac{a}{2 b}) {(- \frac{2 b}{a} x + \frac{2 b}{3})}^{4} + {(\frac{b}{3})}^{3} x}]}_{0}^{a / 2}$
$= \frac{2 M}{a b} [\frac{a}{24 b} {(\frac{2 b}{3})}^{4} - \frac{b}{2 a} {(\frac{a}{2})}^{4} + \frac{b}{3} {(\frac{a}{2})}^{3} - \frac{1}{3} {\frac{1}{4} \cdot \frac{a}{2 b} {(\frac{b}{3})}^{4} - {(\frac{b}{3})}^{3} \frac{a}{2}}]$
$+ \frac{2 M}{a b} [- \frac{b}{2 a} {(\frac{a}{2})}^{4} + \frac{b}{3} {(\frac{a}{2})}^{3} + \frac{1}{3} {\frac{1}{4} \cdot (- \frac{a}{2 b}) {(\frac{b}{3})}^{4} + {(\frac{b}{3})}^{3} \frac{a}{2}} + \frac{a}{24 b} {(\frac{2 b}{3})}^{4}]$
$= 2 \cdot \frac{2 M}{a b} (\frac{a}{24 b} \cdot \frac{16 b^{4}}{81} - \frac{b}{2 a} \cdot \frac{a^{4}}{16} + \frac{b}{3} \cdot \frac{a^{3}}{8} - \frac{a}{24 b} \cdot \frac{b^{4}}{81} + \frac{a}{6} \cdot \frac{b^{3}}{27})$
$= \frac{4 M}{a b} (\frac{a^{3} b}{2^{5} \cdot 3} + \frac{a b^{3}}{2^{3} \cdot 3^{2}})$ $= \frac{M}{6} (\frac{a^{2}}{4} + \frac{b^{2}}{3})$

となる．

解説2

★ 直交軸の定理を用いて計算

剛体が薄い平板の場合，直交軸の定理を適用できる．図のように座標軸をとり， $x y$ 面に置かれた二等辺三角形の薄板について，質量中心を通る $z$ 軸のまわりの慣性モーメント $I_{z}$ を考える．二等辺三角形の薄板の慣性モーメント1より， $y$ 軸のまわりの慣性モーメント $I_{y}$ は

$I_{y} = \frac{M a^{2}}{24}$

である．また，二等辺三角形の薄板の慣性モーメント2より， $x$ 軸のまわりの慣性モーメント $I_{x}$ は

$I_{x} = \frac{M b^{2}}{18}$

である．したがって，直交軸の定理より

$I_{z} = I_{x} + I_{y}$ $= \frac{M b^{2}}{18} + \frac{M a^{2}}{24}$ $= \frac{M}{6} (\frac{a^{2}}{4} + \frac{b^{2}}{3})$

閉じる解説トップへ

ホーム>>物理演習問題>>力学>>剛体の力学>>慣性モーメント>>二等辺三角形の薄板の慣性モーメント3

最終更新日：2026年1月12日