球殻の慣性モーメント

半径 ${\displaystyle R}$ の薄い球殻の表面積は ${\displaystyle 4\pi R^2}$ なので，球殻の面密度を ${\displaystyle \sigma }$ とすると

${\displaystyle \sigma =\frac{M}{4\pi R^2}}$

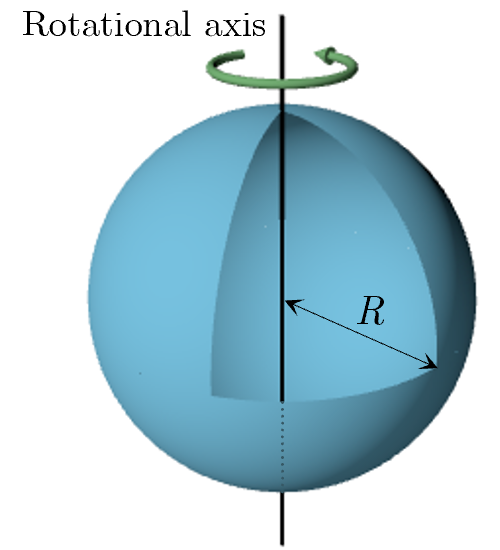
である．図に示すように，回転軸を ${\displaystyle z}$ 軸にとり，この球を ${\displaystyle z}$ 軸方向に微小幅 ${\displaystyle dz}$ でスライスし，多数の円環に分割する． ${\displaystyle z}$ 方向の位置 ${\displaystyle z}$ における円環の半径は ${\displaystyle x=\sqrt{R^2-z^2}}$ である．この円環の表面積 ${\displaystyle dS}$ を求める場合，図の赤枠で示しているように傾斜していることを考慮しなければならず，その斜辺の長さ ${\displaystyle \sqrt{{(dx)}^2+{(dz)}^2}}$ より

${\displaystyle dS=2\pi x\cdot \sqrt{{(dx)}^2+{(dz)}^2}}$

となる．ここで，

${\displaystyle \frac{dx}{dz}=-\frac{z}{\sqrt{R^2-z^2}}=-\frac{z}{x}}$

なので，

${\displaystyle \sqrt{{(dx)}^2+{(dz)}^2}=dz\sqrt{{\left(\frac{dx}{dz}\right)}^2+1}}$ ${\displaystyle =dz\sqrt{{\left(-\frac{z}{x}\right)}^2+1}}$ ${\displaystyle =\frac{\sqrt{x^2+z^2}}{x}dz}$ ${\displaystyle =\frac{R}{x}dz}$

である．よって，円環の表面積は

${\displaystyle dS=2\pi x\cdot \frac{R}{x}dz}$ ${\displaystyle =2\pi Rdz}$

であり，この円環の質量を ${\displaystyle dm}$ とおくと

${\displaystyle dm=\sigma dS}$ ${\displaystyle =\frac{M}{4\pi R^2}\cdot 2\pi Rdz}$ ${\displaystyle =\frac{M}{2R}dz}$

となる．この円環の慣性モーメント ${\displaystyle dI}$ は，質量中心を通り面に垂直な回転軸周りの薄い円筒の慣性モーメント（ ${\displaystyle I=M{R}^2}$ ）より

${\displaystyle dI=dm\cdot x^2}$ ${\displaystyle =\frac{M}{2R}dz\cdot (R^2-z^2)}$ ${\displaystyle =\frac{M}{2R}(R^2-z^2)dz}$

となる．したがって，求める慣性モーメント ${\displaystyle I}$ は

${\displaystyle I={\displaystyle {\int }_{D}dI}}$ ${\displaystyle ={\displaystyle {\int }_{-R}^R\frac{M}{2R}(R^2-z^2)dz}}$ ${\displaystyle =\frac{M}{2R}{[R^{2}z-\frac{1}{3}{z}^3]}_{-R}^R}$ ${\displaystyle =M{R}^2(1-\frac{1}{3})}$ ${\displaystyle =\frac{2}{3}M{R}^2}$

となる．

★ 極座標を用いて計算

図に示すように，球殻を多数の微小面積に分割し，極座標 ${\displaystyle (R,\theta ,\varphi )}$ を用いて，微小面積を表すと

${\displaystyle dS=Rd\theta \cdot R\sin \theta d\varphi }$
${\displaystyle \phantom{dS}=R^2\sin \theta d\theta d\varphi }$

となるので，球殻の面密度

${\displaystyle \sigma =\frac{M}{4\pi R^2}}$

より，この微小面積の質量は

${\displaystyle dm=\sigma dS}$ ${\displaystyle =\frac{M}{4\pi }\sin \theta d\theta d\varphi }$

である．この微小部分の回転軸までの距離（回転半径）は ${\displaystyle R\sin \theta }$ なので，微小面積の回転軸周りの慣性モーメント ${\displaystyle dI}$ は

${\displaystyle dI={(R\sin \theta )}^{2}dm}$ ${\displaystyle =\frac{M{R}^2}{4\pi }{\sin }^3\theta d\theta d\varphi }$

と表せる．したがって，求める慣性モーメント ${\displaystyle I}$ は，

${\displaystyle I={\displaystyle {\int }_{D}dI}}$ ${\displaystyle ={\displaystyle {\int }_0^{\pi }{\displaystyle {\int }_0^{2\pi }\frac{M{R}^2}{4\pi }{\sin }^3\theta d\theta d\varphi }}}$ ${\displaystyle =\frac{M{R}^2}{4\pi }{\displaystyle {\int }_0^{\pi }{\sin }^3\theta d\theta }{\displaystyle {\int }_0^{2\pi }d\varphi }}$

となる．各々の積分は

${\displaystyle {\displaystyle {\int }_0^{\pi }{\sin }^3\theta d\theta }={\displaystyle {\int }_0^{\pi }(1-{\cos }^2\theta )\sin \theta d\theta }}$   （${\displaystyle u=\cos \theta }$ とおいて置換積分）
     ${\displaystyle ={\displaystyle {\int }_{-1}^1(1-u^2)du}}$ ${\displaystyle ={[u-\frac{1}{3}{u}^3]}_{-1}^1}$ ${\displaystyle =2-\frac{2}{3}=\frac{4}{3}}$
${\displaystyle {\displaystyle {\int }_0^{2\pi }d\varphi }={\left[\varphi \right]}_0^{2\pi }=2\pi }$

なので，慣性モーメントは

${\displaystyle I=\frac{M{R}^2}{4\pi }\cdot \frac{4}{3}\cdot 2\pi }$ ${\displaystyle =\frac{2}{3}M{R}^2}$

と求まる．