等加速度直線運動の式の導出（積分から求める） (derivation of motion expression by integration)

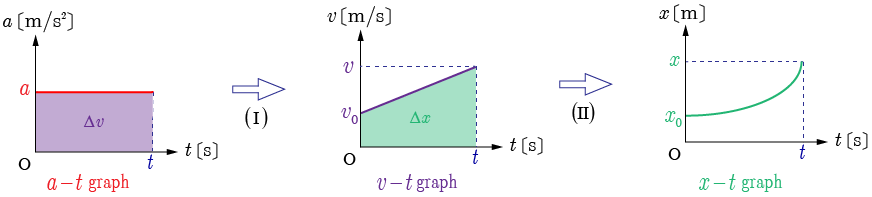
時刻 ${\displaystyle t〔\mathrm{s}〕}$ での位置，速度，加速度をそれぞれ ${\displaystyle x\left(t\right)〔\text{m}〕}$  ， ${\displaystyle v\left(t\right)〔\text{m}/\text{s}〕}$  ， ${\displaystyle a\left(t\right)〔\text{m}/{\text{s}}^2〕}$   とする．

物体が等加速度直線運動をしているとき，物体の加速度は一定 ( ${\displaystyle a=\text{const}}$ )である． 初期条件を用いて積分することで(位置，速度，加速度の関係)任意の時刻 ${\displaystyle t〔\mathrm{s}〕}$ での位置 ${\displaystyle x\left(t\right)〔\text{m}〕}$   と速度 ${\displaystyle v\left(t\right)〔\text{m}/\text{s}〕}$   を導出することができる．

初期条件：時刻 ${\displaystyle t=0\text{s}}$   での速度を ${\displaystyle v(0)=v_0〔\text{m}/\text{s}〕}$   ，位置を ${\displaystyle x(0)=x_0〔\text{m}〕}$   とする．

${\displaystyle \left(\mathrm{I}\right)}$ 速度 ${\displaystyle v〔\text{m}/\text{s}〕}$ は以下のように積分することで求めることができる．

${\displaystyle v={\displaystyle \int adt}=at+C_1}$

${\displaystyle t=0\text{s}}$   のとき ${\displaystyle v=v_0〔\text{m}/\text{s}〕}$ を上式に代入して ${\displaystyle C_1=v_0}$ が得られる．

よって速度 ${\displaystyle v〔\text{m}/\text{s}〕}$ は

${\displaystyle v=v_0+at}$

と表される．

${\displaystyle \left(\mathrm{II}\right)}$ 位置 ${\displaystyle x〔\text{m}〕}$ は以下のように積分して求めることができる．

${\displaystyle x={\displaystyle \int vdt}=v_{0}t+\frac{1}{2}a{t}^2+C_2}$

${\displaystyle t=0\text{s}}$   のとき ${\displaystyle x=x_0〔\text{m}〕}$ を上式に代入して ${\displaystyle C_2=x_0}$ が得られる．

よって位置 ${\displaystyle x〔\text{m}〕}$ は

${\displaystyle x=x_0+v_{{}_0}t+\frac{1}{2}a{t}^2}$

と表される．

ホーム>>物理基礎>>第1編 物体の運動とエネルギー>>第1章　物体の運動>>等加速度直線運動の式の導出（積分で求める）

学生スタッフ作成

最終更新日： 2018年3月5日