ヤングの干渉実験

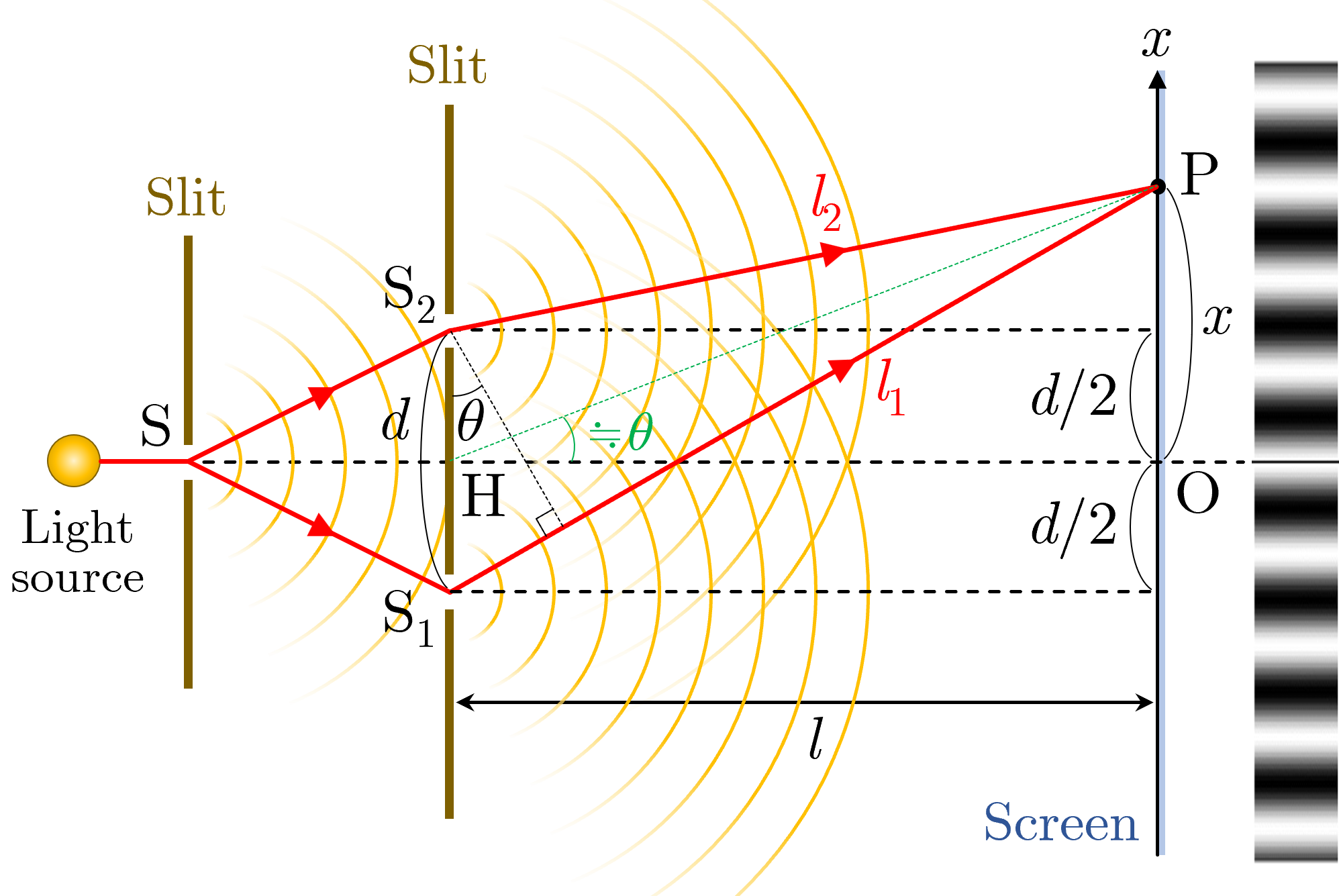
図のように，光源から出て単スリット ${\displaystyle \text{S}}$ を通った波長 ${\displaystyle \lambda }$ の単色光は，複スリット ${\displaystyle {\text{S}}_1}$ ， ${\displaystyle {\text{S}}_2}$ で回折し，光波は ${\displaystyle {\text{S}}_1}$ ， ${\displaystyle {\text{S}}_2}$ を新たな2つの波源として干渉し，スクリーン上の点 ${\displaystyle \text{P}}$ で回折像（明暗の干渉縞）を生じる．

複スリットの間隔 ${\displaystyle \overline{{\text{S}}_{\text{1}}{\text{S}}_{\text{2}}}=d}$ ，複スリットからスクリーンまでの距離 ${\displaystyle \overline{\text{Q}\text{O}}=l}$ ，スクリーン上の原点 ${\displaystyle \text{O}}$ から点 ${\displaystyle \text{P}}$ までの距離 ${\displaystyle \overline{\text{OP}}=x}$ を用いて，明線と暗線の位置は次式で表される．

明線の位置： ${\displaystyle x=m\frac{l\lambda }{d}}$
暗線の位置： ${\displaystyle x=\left(m+\frac{1}{2}\right)\frac{l\lambda }{d}}$

（整数 ${\displaystyle m=0,\pm 1,\pm 2,\cdots }$ ）

ここで， ${\displaystyle \overline{\text{S}{\text{S}}_{\text{1}}}=\overline{\text{S}{\text{S}}_{\text{2}}}}$ ， ${\displaystyle \overline{{\text{S}}_{\text{1}}\text{O}}=\overline{{\text{S}}_{\text{2}}\text{O}}}$ である．また，実際の距離は概ね ${\displaystyle d\approx 1\text{mm}}$ ， ${\displaystyle x\approx 1\text{mm}-1\text{cm}}$ ， ${\displaystyle l\approx 1\text{m}}$ 程度であり， ${\displaystyle \text{l}\gg d,x}$ なので，図では平行に見えないが線分 ${\displaystyle {\text{S}}_{\text{1}}\text{P}}$ と ${\displaystyle {\text{S}}_{\text{2}}\text{P}}$ はほぼ平行とみなせる．

スクリーン上の原点 ${\displaystyle \text{O}}$ の位置は明るい縞模様となる．原点 ${\displaystyle \text{O}}$ から ${\displaystyle m}$ 番目， ${\displaystyle \left(m+1\right)}$ 番目までの明線の位置を ${\displaystyle x_m}$ ， ${\displaystyle x_{m+1}}$ とすると，明線の間隔は

${\displaystyle \Delta x=x_{m+1}-x_m=\left(m+1\right)\frac{l\lambda }{d}-m\frac{l\lambda }{d}}$ ${\displaystyle =\frac{l\lambda }{d}}$ ＝ 一定

となる．したがって， ${\displaystyle l}$ , ${\displaystyle d}$ , ${\displaystyle \Delta x}$ を測定すれば，

${\displaystyle \lambda =\frac{d\Delta x}{l}}$

より光の波長 ${\displaystyle \lambda }$ が求まる．

光路差 ${\displaystyle \Delta l=l_1-l_2}$ を求め，干渉条件（明線と暗線が生じる条件）を考えよう．三平方の定理より

${\displaystyle \overline{{\text{S}}_{\text{1}}\text{P}}=l_1}$ ${\displaystyle =\sqrt{l^2+{\left(x+\frac{d}{2}\right)}^2}}$ ${\displaystyle =l{\left\{1+{\left(\frac{x+d/2}{l}\right)}^2\right\}}^{\frac{1}{2}}}$   ---(1)
${\displaystyle \overline{{\text{S}}_{\text{2}}\text{P}}=l_2}$ ${\displaystyle =\sqrt{l^2+{\left(x-\frac{d}{2}\right)}^2}}$ ${\displaystyle =l{\left\{1+{\left(\frac{x-d/2}{l}\right)}^2\right\}}^{\frac{1}{2}}}$   ---(2)

であり， ${\displaystyle \left|a\right|\ll 1}$ のときの近似式* ${\displaystyle {(1+a)}^{\frac{1}{2}}\approx 1+\frac{1}{2}a}$ を用いると，式(1),(2)は

(1) ⇒ ${\displaystyle l_1\approx l\left\{1+\frac{1}{2}{\left(\frac{x+d/2}{l}\right)}^2\right\}}$ ${\displaystyle =l+\frac{1}{2l}\left(x^2+xd+\frac{d^2}{4}\right)}$   ---(3)
(2) ⇒ ${\displaystyle l_1\approx l\left\{1+\frac{1}{2}{\left(\frac{x-d/2}{l}\right)}^2\right\}}$ ${\displaystyle =l+\frac{1}{2l}\left(x^2-xd+\frac{d^2}{4}\right)}$   ---(4)

と近似できる．したがって，(3)-(4)より光路差は

${\displaystyle \Delta l=l_1-l_2}$ ${\displaystyle \approx \frac{xd}{2l}-\left(-\frac{xd}{2l}\right)=\frac{d}{l}x}$

と求まる．光路差が半波長の偶数倍であれば強め合って明線となり，奇数倍であれば弱め合って暗線となる．よって，干渉条件（ ${\displaystyle m}$ ：整数）

明線： ${\displaystyle \Delta l=2m\cdot \frac{\lambda }{2}=m\lambda }$
暗線： ${\displaystyle \Delta l=(2m+1)\cdot \frac{\lambda }{2}=\left(m+\frac{1}{2}\right)\lambda }$

から，上述の明線と暗線の位置が求まる．

＜光路差 ${\displaystyle \Delta l}$ の別の求め方＞

ホーム>>物理>>第3編　波>>第3章　光>>ヤングの干渉実験

学生スタッフ作成

最終更新日： 2025年10月24日