薄いプリズムを透過した光線の偏角

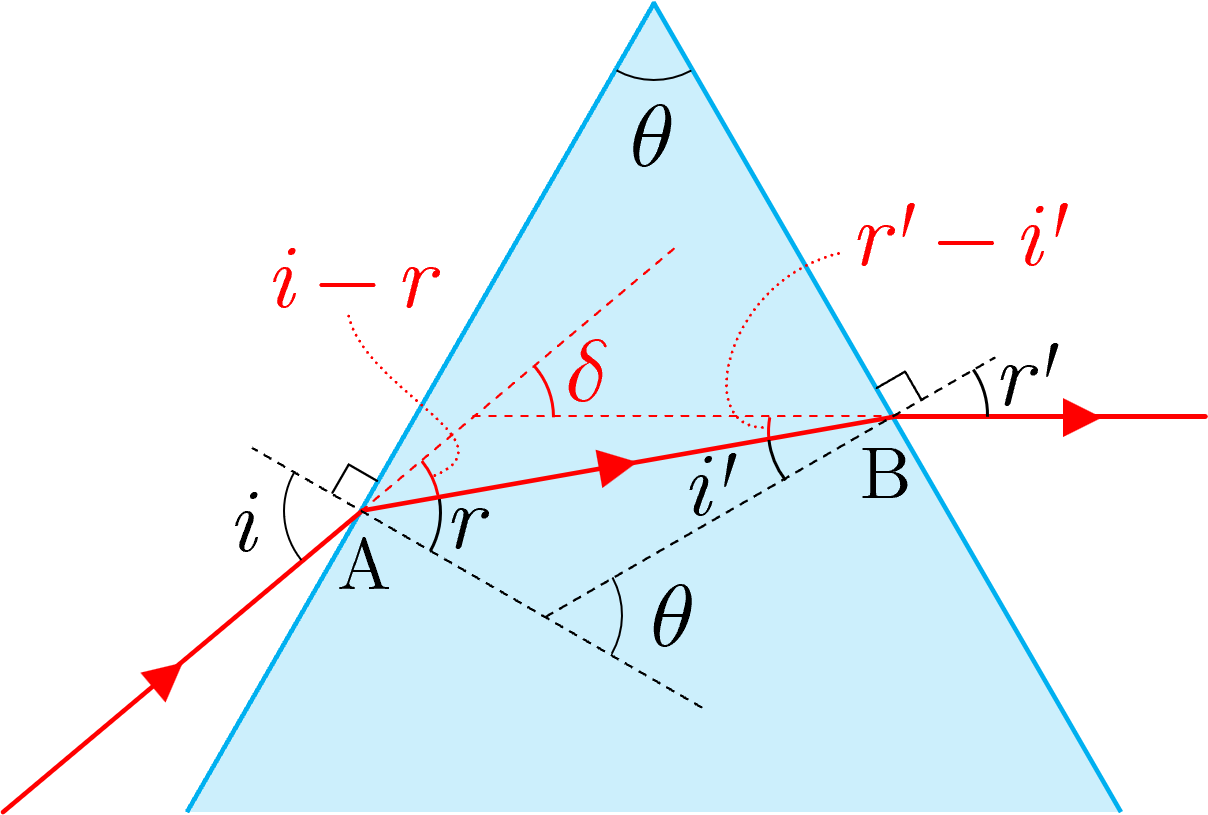
図のように，頂角 ${\displaystyle \theta }$ が十分小さい楔（くさび）型の薄いプリズム（屈折率 ${\displaystyle n}$ ）に十分小さな入射角 ${\displaystyle i}$ で単色光が入射するとき，プリズムの点Aに入射する光線と点Bから透過する光線との間の角 ${\displaystyle \delta }$ （偏角 (angle of deviation)） は近似的に

${\displaystyle \delta \approx (n-1)\theta }$

とみなせる．（※ 図では見やすいように頂角 ${\displaystyle \theta }$ や入射角 ${\displaystyle i}$ を大きく描いているが，上式が成立するのは ${\displaystyle \sin \theta \approx \theta }$ , ${\displaystyle \sin i\approx i}$ と近似できるくらいの小さな角度である．）

屈折率 ${\displaystyle 1.5}$ のガラスでできた薄いプリズムの場合， ${\displaystyle \delta \approx 0.5\theta }$ より偏角 ${\displaystyle \delta }$ は頂角 ${\displaystyle \theta }$ のおよそ半分となる．

＜証明＞
点Aでの入射角 ${\displaystyle i}$ と屈折角 ${\displaystyle r}$ について，屈折の法則は

${\displaystyle \frac{\sin i}{\sin r}=n}$

であり， ${\displaystyle i}$ が十分小さい場合 ${\displaystyle r}$ も十分小さいとみなせるので ${\displaystyle \sin i\approx i}$ , ${\displaystyle \sin r\approx r}$ より上式から

${\displaystyle i\approx nr}$ --- (1)

となる．同様に点Bでの入射角 ${\displaystyle i^{\prime }}$ と屈折角 ${\displaystyle r^{\prime }}$ について，屈折の法則は

${\displaystyle \frac{\sin i^{\prime }}{\sin r^{\prime }}=\frac{1}{n}}$

であり， ${\displaystyle \theta }$ と ${\displaystyle r}$ が十分小さければ ${\displaystyle i^{\prime }}$ と ${\displaystyle r^{\prime }}$ も十分小さいので ${\displaystyle \sin i^{\prime }\approx i^{\prime }}$ , ${\displaystyle \sin r^{\prime }\approx r^{\prime }}$ より

${\displaystyle r^{\prime }\approx n{i}^{\prime }}$ --- (2)

となる．また，図において三角形の外角の性質より

${\displaystyle \theta =r+i^{\prime }}$ --- (3)
${\displaystyle \delta =i-r+r^{\prime }-i^{\prime }}$ --- (4)

である．式(1),(2),(3)を用いると式(4)は

${\displaystyle \delta =i+r^{\prime }-(r+i^{\prime })}$ ${\displaystyle \approx n(r+i^{\prime })-(r+i^{\prime })}$ ${\displaystyle =n\theta -\theta }$ ${\displaystyle =(n-1)\theta }$

となる．

※ 補足
下の図の場合も考え方は全く同じである．

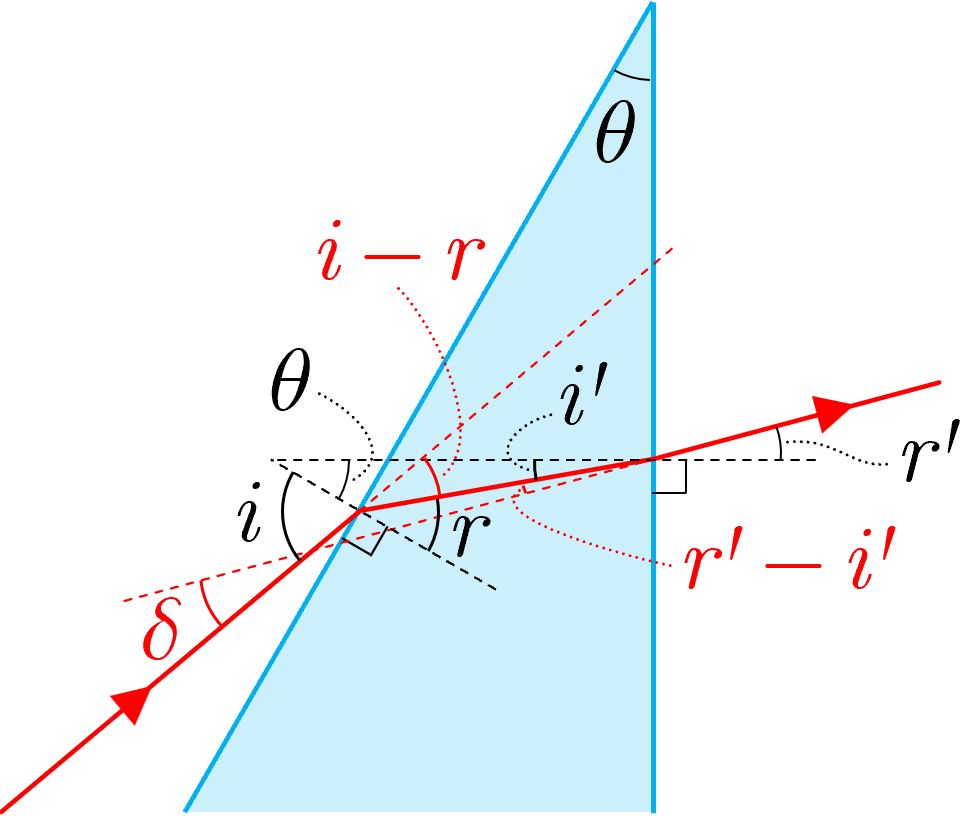
図において三角形の外角の性質より

${\displaystyle \theta +i^{\prime }=r}$ --- (5)
${\displaystyle \delta +r^{\prime }-i^{\prime }=i-r}$ --- (6)

なので，式(1),(2),(5)を用いると式(6)は

${\displaystyle \delta =i-r^{\prime }-(r-i^{\prime })}$ ${\displaystyle \approx n(r-i^{\prime })-(r-i^{\prime })}$ ${\displaystyle =n\theta -\theta }$ ${\displaystyle =(n-1)\theta }$

となる．

ホーム>>物理>>第3編　波>>第3章　光>>薄いプリズムを透過した光線の偏角

学生スタッフ作成

最終更新日： 2025年10月24日