レンズ (lens)

レンズ (lens) とは，光を屈折させて収束や発散させる光学素子のことであり，その多くは2つの球面で囲まれたガラスなどの透明体でできており，その2つの球面の中心を結ぶ直線を光軸 (optical axis) という．レンズには，中心部が周辺部より厚い凸レンズ (convex lens)（光を収束させる）と，中心部が周辺部より薄い凹レンズ (concave lens)（光を発散させる）がある．

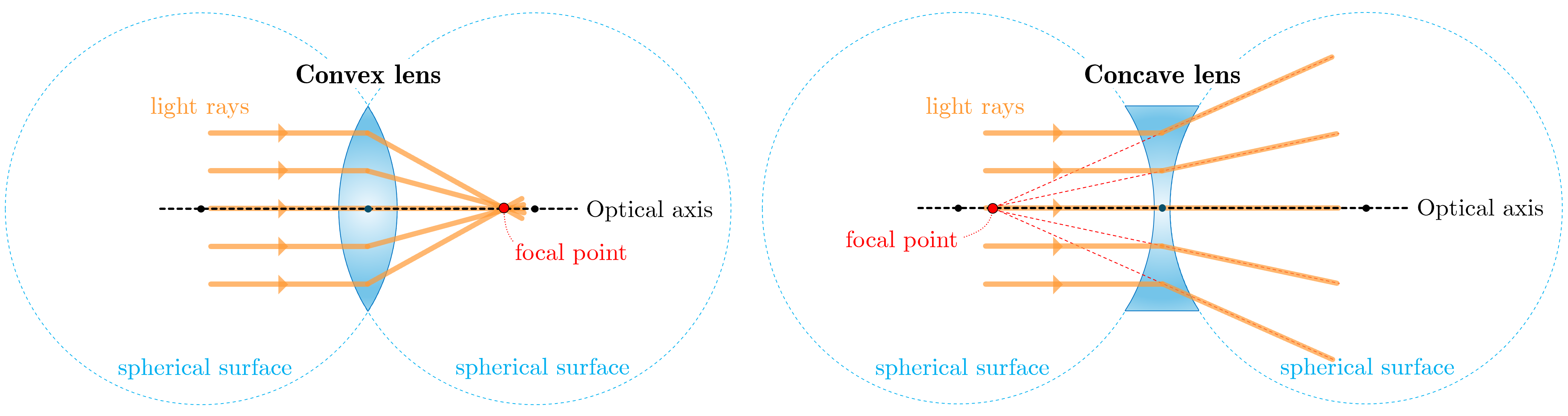
光軸に平行な光を凸レンズに当てると，レンズの両面で屈折し，レンズの後方の光軸上の1点を通過する．この点を凸レンズの焦点 (focal point) といい，レンズの中心から焦点までの距離を焦点距離という．逆行する光は同じ経路を通るので，焦点を通ってレンズに入る光は，レンズ通過後は光軸に平行に進む．焦点はレンズの前後に1つずつあり，薄いレンズでは，それらの焦点距離が等しい．

凹レンズの場合，光軸に平行な光を当てると，レンズ後方の光は，レンズ前方の光軸上の1点から出たように進む．この点を凹レンズの焦点という．逆にレンズ後方の焦点に向かって進む光は，レンズ通過後，光軸に平行に進む．

■ 凸レンズによる実像

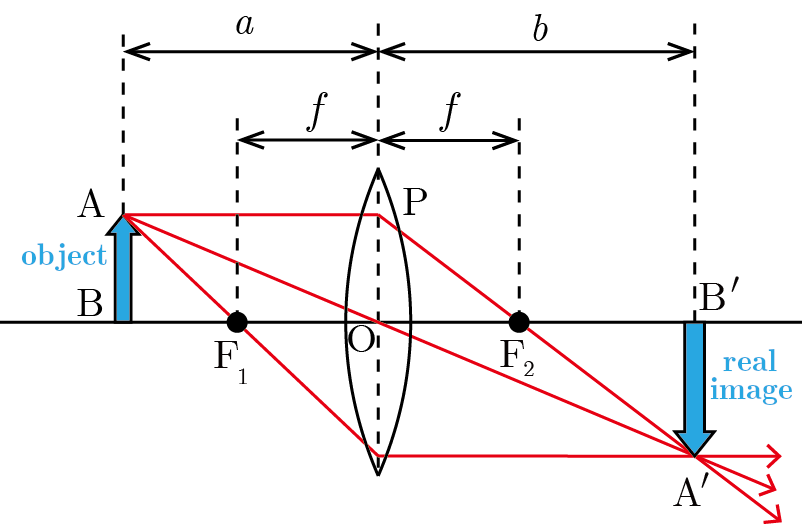
図のように，凸レンズの焦点 ${\displaystyle {\text{F}}_1}$ の外側に物体 ${\displaystyle \text{AB}}$ を置くと，レンズ後方のある位置に倒立像 ${\displaystyle {\text{A}}^{\prime }{\text{B}}^{\prime }}$ が生じる．この像は，実際に物体からの光が集まってできる像なので，実像 (real image) という．

凸レンズと物体 ${\displaystyle \text{AB}}$ との距離を ${\displaystyle a}$ ，凸レンズと実像 ${\displaystyle {\text{A}}^{\prime }{\text{B}}^{\prime }}$ との距離を ${\displaystyle b}$ ，凸レンズの焦点距離を ${\displaystyle f}$ とすると，以下の関係式

${\displaystyle \frac{1}{a}+\frac{1}{b}=\frac{1}{f}}$     ······ (1)

を満たす．これは物体と生じる像の位置関係を表す式で写像公式という．

写像公式(1)の導出（クリックで開く）

${\displaystyle △\text{ABO}}$ と ${\displaystyle △{\text{A}}^{\prime }{\text{B}}^{\prime }\text{O}}$ は相似なので

${\displaystyle \frac{{\text{A}}^{\prime }{\text{B}}^{\prime }}{\text{AB}}=\frac{{\text{B}}^{\prime }\text{O}}{\text{BO}}=\frac{b}{a}}$     ······ ①

であり， ${\displaystyle △{\text{POF}}_2}$ と ${\displaystyle △{\text{A}}^{\prime }{\text{B}}^{\prime }{\text{F}}_2}$ も相似なので

${\displaystyle \frac{{\text{A}}^{\prime }{\text{B}}^{\prime }}{\text{PO}}=\frac{{\text{B}}^{\prime }{\text{F}}_2}{\text{O}{\text{F}}_2}=\frac{b-f}{f}}$     ······ ②

である． ${\displaystyle \text{AB}=\text{PO}}$ より，① ＝ ② が成り立つので

${\displaystyle \frac{b}{a}=\frac{b-f}{f}}$   ⇔   ${\displaystyle \frac{1}{a}=\frac{1}{f}-\frac{1}{b}}$   ⇔   ${\displaystyle \frac{1}{a}+\frac{1}{b}=\frac{1}{f}}$

が得られる．

物体の大きさに対する像の大きさの比を倍率といい，次式で表される．

倍率 ${\displaystyle m=\frac{{\text{A}}^{\prime }{\text{B}}^{\prime }}{\text{AB}}=\frac{b}{a}}$

■ 凸レンズによる虚像

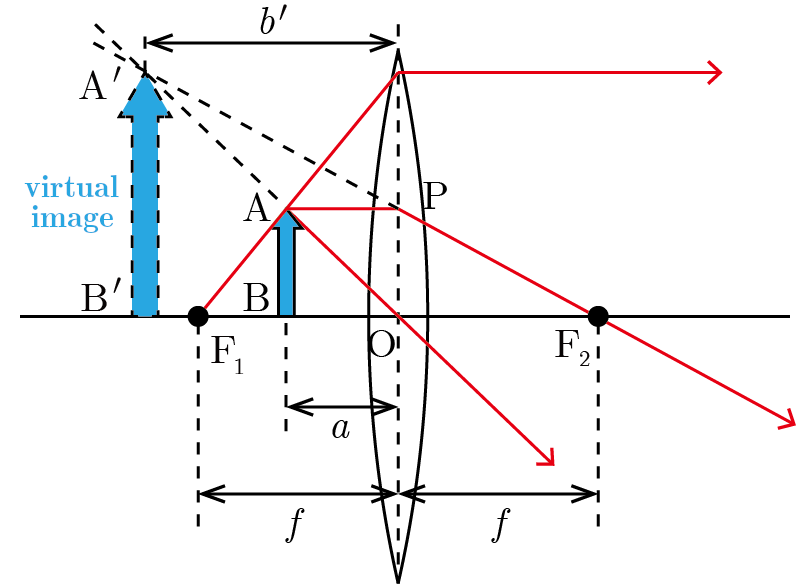
図のように，凸レンズの焦点 ${\displaystyle {\text{F}}_1}$ の内側に物体 ${\displaystyle \text{AB}}$ を置いて，レンズの後方から物体 ${\displaystyle \text{AB}}$ を覗き見ると，あたかも ${\displaystyle {\text{A}}^{\prime }{\text{B}}^{\prime }}$ のように拡大されて見える．この像は，実際には光が集まって生じた像ではないので，虚像 (virtual image) といい，倒立していないので正立像である．

凸レンズと物体 ${\displaystyle \text{AB}}$ との距離を ${\displaystyle a}$ ，凸レンズと虚像 ${\displaystyle {\text{A}}^{\prime }{\text{B}}^{\prime }}$ との距離を ${\displaystyle b^{\prime }}$ ，凸レンズの焦点距離を ${\displaystyle f}$ とすると，以下の関係式

${\displaystyle \frac{1}{a}-\frac{1}{b^{\prime }}=\frac{1}{f}}$     ······ (2)

を満たす．これは写像公式(1)に ${\displaystyle b=-b^{\prime }}$ を代入すれば求まるため，虚像の場合は ${\displaystyle b<0}$ となると考えればよい．また，倍率 ${\displaystyle m}$ は

${\displaystyle m=\frac{{\text{A}}^{\prime }{\text{B}}^{\prime }}{\text{AB}}=\frac{b^{\prime }}{a}}$

である．焦点距離 ${\displaystyle f}$ は正なので，(2)より ${\displaystyle a<b^{\prime }}$ となり，倍率 ${\displaystyle m>1}$ である（拡大される）．

写像公式(2)の導出（クリックで開く）

${\displaystyle △\text{ABO}}$ と ${\displaystyle △{\text{A}}^{\prime }{\text{B}}^{\prime }\text{O}}$ は相似なので

${\displaystyle \frac{{\text{A}}^{\prime }{\text{B}}^{\prime }}{\text{AB}}=\frac{{\text{B}}^{\prime }\text{O}}{\text{BO}}=\frac{b^{\prime }}{a}}$     ······ ③

であり， ${\displaystyle △{\text{POF}}_2}$ と ${\displaystyle △{\text{A}}^{\prime }{\text{B}}^{\prime }{\text{F}}_2}$ も相似なので

${\displaystyle \frac{{\text{A}}^{\prime }{\text{B}}^{\prime }}{\text{PO}}=\frac{{\text{B}}^{\prime }{\text{F}}_2}{\text{O}{\text{F}}_2}=\frac{b^{\prime }+f}{f}}$     ······ ④

である． ${\displaystyle \text{AB}=\text{PO}}$ より，③ ＝ ④ が成り立つので

${\displaystyle \frac{b^{\prime }}{a}=\frac{b^{\prime }+f}{f}}$   ⇔   ${\displaystyle \frac{1}{a}=\frac{1}{f}+\frac{1}{b^{\prime }}}$   ⇔   ${\displaystyle \frac{1}{a}-\frac{1}{b^{\prime }}=\frac{1}{f}}$

が得られる．

■ 凹レンズによる虚像

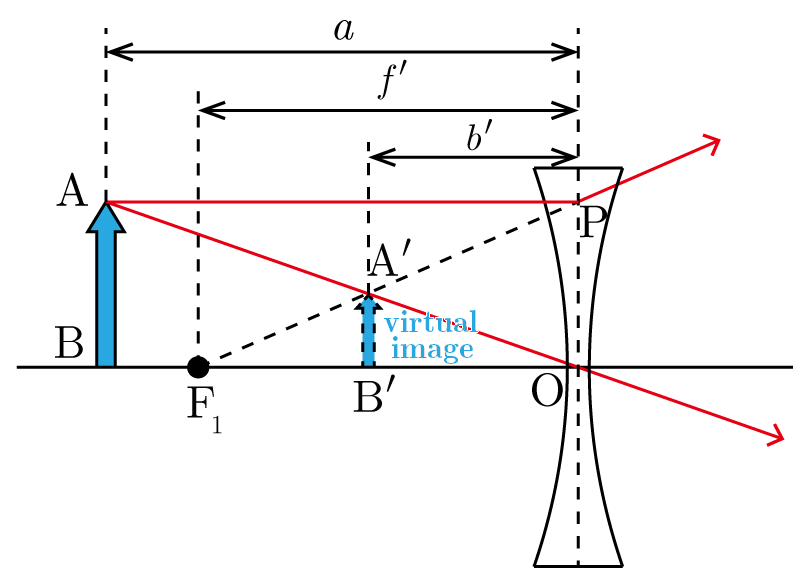
図のように，凹レンズの前方に物体 ${\displaystyle \text{AB}}$ を置いて，レンズの後方から物体 ${\displaystyle \text{AB}}$ を覗き見ると，あたかも ${\displaystyle {\text{A}}^{\prime }{\text{B}}^{\prime }}$ のように縮小されて見える．この像は，実際には光が集まって生じた像ではないので虚像であり，物体が焦点より近くても遠くても実像はできず，常にレンズ越しに正立像が見える．

凹レンズと物体 ${\displaystyle \text{AB}}$ との距離を ${\displaystyle a}$ ，凹レンズと虚像 ${\displaystyle {\text{A}}^{\prime }{\text{B}}^{\prime }}$ との距離を ${\displaystyle b^{\prime }}$ ，凹レンズの焦点距離を ${\displaystyle f^{\prime }}$ とすると，以下の関係式

${\displaystyle \frac{1}{a}-\frac{1}{b^{\prime }}=-\frac{1}{f^{\prime }}}$     ······ (3)

を満たす．これは写像公式(1)に ${\displaystyle b=-b^{\prime }}$ ，及び ${\displaystyle f=-f^{\prime }}$ を代入すれば求まるため，凹レンズの場合は ${\displaystyle f<0}$ となると考えればよい．また，倍率 ${\displaystyle m}$ は

${\displaystyle m=\frac{{\text{A}}^{\prime }{\text{B}}^{\prime }}{\text{AB}}=\frac{b^{\prime }}{a}}$

である．焦点距離 ${\displaystyle f^{\prime }}$ は正なので，(3)より ${\displaystyle a>b^{\prime }}$ となり，倍率 ${\displaystyle m<1}$ である（縮小される）．

写像公式(3)の導出（クリックで開く）

${\displaystyle △\text{ABO}}$ と ${\displaystyle △{\text{A}}^{\prime }{\text{B}}^{\prime }\text{O}}$ は相似なので

${\displaystyle \frac{{\text{A}}^{\prime }{\text{B}}^{\prime }}{\text{AB}}=\frac{{\text{B}}^{\prime }\text{O}}{\text{BO}}=\frac{b^{\prime }}{a}}$     ······ ⑤

であり， ${\displaystyle △{\text{POF}}_1}$ と ${\displaystyle △{\text{A}}^{\prime }{\text{B}}^{\prime }{\text{F}}_1}$ も相似なので

${\displaystyle \frac{{\text{A}}^{\prime }{\text{B}}^{\prime }}{\text{PO}}=\frac{{\text{B}}^{\prime }{\text{F}}_1}{\text{O}{\text{F}}_1}=\frac{f^{\prime }-b^{\prime }}{f^{\prime }}}$     ······ ⑥

である． ${\displaystyle \text{AB}=\text{PO}}$ より，⑤ ＝ ⑥ が成り立つので

${\displaystyle \frac{b^{\prime }}{a}=\frac{f^{\prime }-b^{\prime }}{f^{\prime }}}$   ⇔   ${\displaystyle \frac{1}{a}=\frac{1}{b^{\prime }}-\frac{1}{f^{\prime }}}$   ⇔   ${\displaystyle \frac{1}{a}-\frac{1}{b^{\prime }}=-\frac{1}{f^{\prime }}}$

が得られる．

◎ レンズにおける光線の作図

上述のレンズによって生じる像の位置は，以下のレンズを通る光の性質を使って，作図により求めることができる．

• レンズの中心を通る光は直進する
• 凸レンズの場合，光軸に平行な光がレンズに入射すると，レンズの後方で焦点を通る
• 凹レンズの場合，光軸に平行な光がレンズに入射すると，レンズの前方の焦点から出たように進む

ホーム>>物理>>第3編　波>>第3章　光>>レンズ

学生スタッフ作成

最終更新日： 2025年12月26日