双曲線の問題
■問題
の中心,頂点,漸近線,焦点,離心率を求め,その双曲線を描け.
■答
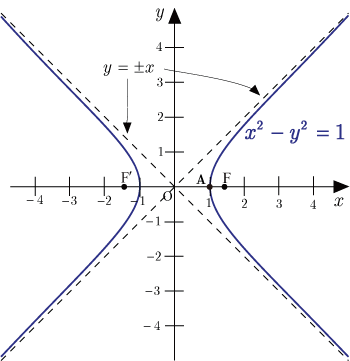
中心:
頂点:,
漸近線: ,
焦点: ,
離心率;
■解き方
最初に
と変形する. 以下の解答はこれを利用する.中心は
頂点は,
漸近線を とすると
, , ,
よって,漸近線は
,
よって
となる.
離心率
となる.グラフは,上記の解答に記す.
ホーム>>カテゴリー分類>>関数>>関数の演習問題>>いろいろな方程式に関する問題>>双曲線の問題
最終更新日: 2024年10月7日
の中心,頂点,漸近線,焦点,離心率を求め,その双曲線を描け.

中心:
頂点:,
漸近線: ,
焦点: ,
離心率;
最初に
と変形する. 以下の解答はこれを利用する.中心は
頂点は,
漸近線を とすると
, , ,
よって,漸近線は
,
よって
となる.
離心率
となる.グラフは,上記の解答に記す.
ホーム>>カテゴリー分類>>関数>>関数の演習問題>>いろいろな方程式に関する問題>>双曲線の問題
最終更新日: 2024年10月7日