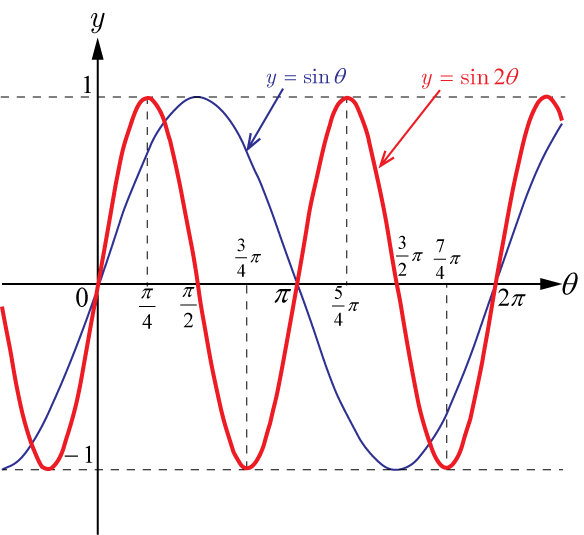
三角関数のグラフに関する問題

■問題

次の三角関数のグラフを描け．

${\displaystyle y=\mathrm{sin2}\theta }$

■解説動画

◆三角関数の動画一覧のページへ

■解答

■ヒント

三角関数のグラフを描くには，基本的な ${\displaystyle \sin \theta ,\cos \theta ,\tan \theta }$ からの拡大や縮小，平行移動を考える．

${\displaystyle y=\sin \beta \theta }$ の場合， ${\displaystyle y=\sin \theta }$ を原点を中心にして ${\displaystyle \theta }$ 軸方向に ${\displaystyle \frac{1}{\beta }}$ 倍 だけ拡大・縮小してグラフを描く．

■解説

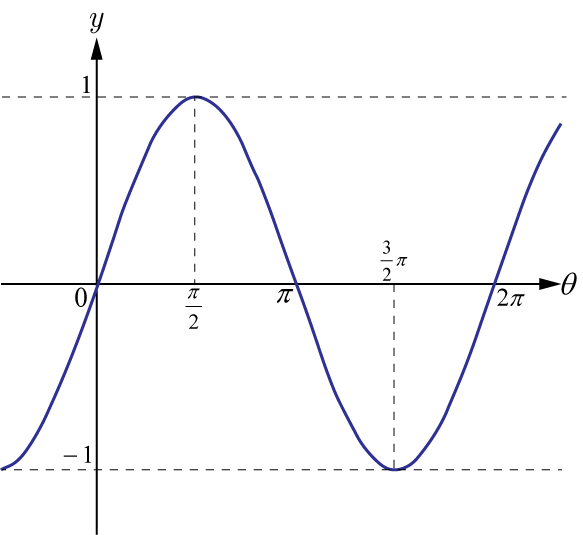
1．基本形である ${\displaystyle y=\sin \theta }$ のグラフを描く．

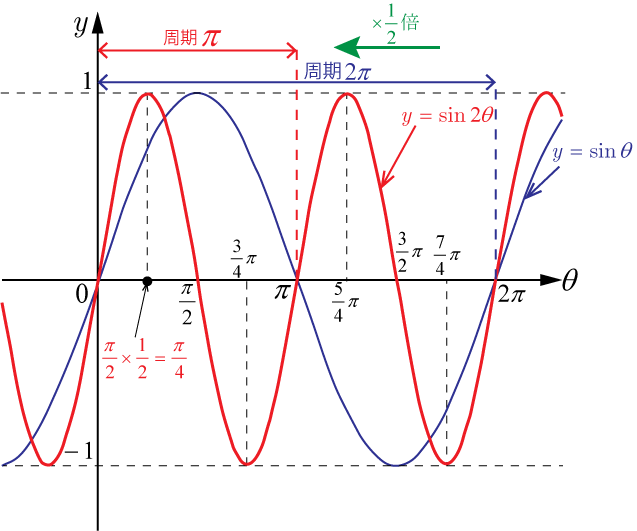
2． ${\displaystyle y=\sin \theta }$ を原点を中心として ${\displaystyle \theta }$ 軸方向に ${\displaystyle \frac{1}{2}}$ 倍に縮小して ${\displaystyle y=\sin 2\theta }$ のグラフを描く．

■各 $\theta$ に対する $2\theta$ ， $\sin \theta$ ， $\sin 2\theta$ の値

■インターラクティブなグラフ

下の画像をクリックしてください．

ホーム>>カテゴリー分類>>三角関数>>三角関数の問題>>三角関数のグラフ>>問題

学生スタッフ作成

最終更新日： 2025年4月27日