ベクトルの計算問題
■問題
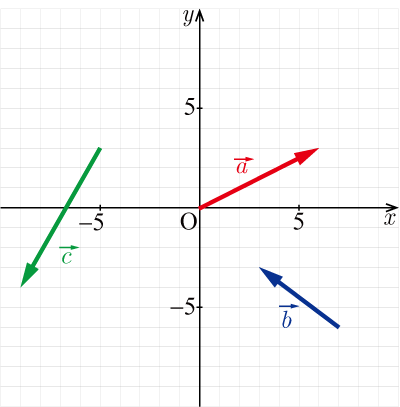
図の , , を成分表示で表し,そのベクトル大きさを求めよ.
■答
,
,
,
■ヒント
ベクトルの成分表示を参照
■解説
● について
の始点の座標は ,終点の座標は である.よって
● について
の始点の座標は ,終点の座標は である.よって
● について
の始点の座標は ,終点の座標は である.よって
ホーム>>カテゴリー分類>>ベクトル>>ベクトルに関する問題>>ベクトルの計算問題
最終更新日: 2025年10月2日

図の , , を成分表示で表し,そのベクトル大きさを求めよ.
,
,
,
ベクトルの成分表示を参照
の始点の座標は ,終点の座標は である.よって
の始点の座標は ,終点の座標は である.よって
の始点の座標は ,終点の座標は である.よって
ホーム>>カテゴリー分類>>ベクトル>>ベクトルに関する問題>>ベクトルの計算問題
最終更新日: 2025年10月2日