重積分の計算問題

■問題

次の重積分の値を求めよ．

${\displaystyle \underset{D}{\iint }xdxdy}$　　${\displaystyle \left(D:0\leqq y\leqq 3x-x^2\right)}$

■答

${\displaystyle \frac{27}{4}}$

■ヒント

はじめに領域 ${\displaystyle D}$を作図し， ${\displaystyle x}$，${\displaystyle y}$ の積分範囲を決定する．

次に， ${\displaystyle x}$ を定数とみなして ${\displaystyle y}$ について積分し，その結果を更に ${\displaystyle x}$ で積分する．

■解説

領域 ${\displaystyle D}$ は

${\displaystyle 0\leqq y\leqq 3x-x^2}$

であることより

直線  ${\displaystyle y=0}$　･･････(1)

曲線  ${\displaystyle y=3x-x^2}$　･･････(2)

で囲まれた領域である．(2)を平方完成すると

${\displaystyle y=-x^2+3x}$

${\displaystyle =-\left(x^2-3x\right)}$

${\displaystyle =-\left\{x^2-3x+{\left(\frac{3}{2}\right)}^2-{\left(\frac{3}{2}\right)}^2\right\}}$

${\displaystyle =-\left\{x^2-3x+{\left(\frac{3}{2}\right)}^2\right\}+{\left(\frac{3}{2}\right)}^2}$

${\displaystyle =-{\left(x^2-\frac{3}{2}\right)}^2+\frac{9}{4}}$

となり，頂点が ${\displaystyle \left(\frac{3}{2},\frac{9}{4}\right)}$ の上に凸のグラフとなることが分かる．

${\displaystyle 3x-x^2=0}$

${\displaystyle x\left(3-x\right)=0}$

${\displaystyle x=0,3}$

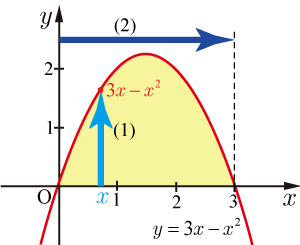
(1)と(2)の交点は ${\displaystyle \left(0,0\right),\left(3,0\right)}$ の2点となる．領域 ${\displaystyle D}$ を作図すると右図のようになる．

これより積分範囲を決定すると

${\displaystyle \underset{D}{\iint }xdxdy}$

${\displaystyle ={\int }_0^3\left({\int }_0^{3x-x^2}xdy\right)dx}$

まず，${\displaystyle {{\displaystyle \int }}_0^{3x-x^2}xdy}$ を計算する．${\displaystyle x}$を定数とみなして${\displaystyle y}$について積分する． 

${\displaystyle ={\int }_0^3{\left[xy\right]}_0^{3x-x^2}dx}$

${\displaystyle ={\int }_0^3\left\{x·\left(3x-x^2\right)-x·0\right\}dx}$

${\displaystyle ={\int }_0^3\left(3x^2-x^3\right)dx}$

更に ${\displaystyle x}$ で積分する． 

${\displaystyle ={\left[x^3-\frac{1}{4}{x}^4\right]}_0^3}$

${\displaystyle =3^3-\frac{1}{4}·3^4-\left(0^3-\frac{1}{4}·0^4\right)}$

${\displaystyle =27-\frac{81}{4}}$

${\displaystyle =\frac{108-81}{4}}$

${\displaystyle =\frac{27}{4}}$

　

　

ホーム>>カテゴリー分類>>積分>>重積分>>重積分の計算問題>>問題

学生スタッフ作成

最終更新日： 2023年8月3日