積分因子の証明
微分方程式
%20%20dx+Q%20%5c(%20x,y%20%20%5c)%20%20dy=0}) について
について
(2)
%20%20-%20%5chspace{1}{Q}_{x}%20%5c(%20x,y%20%20%5c)%20%20%20%20%5chspace{2}}{%5chspace{2}%20P%20%5c(%20x,y%20%20%5c)%20%20%20%20%5chspace{2}}={%5cvarphi}%20%5c(y%5c)%20%20}) (
(
 だけの関数)ならば,
だけの関数)ならば,
%20%20dy%20%20%20%20}%20%20}}) は積分因子である.
は積分因子である.
■証明
 ・・・・・・(1)
・・・・・・(1)
(1)の両辺に
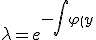%20%20dy%20%20%20%20}%20%20}}) をかける.
をかける.
%20%20=0})
%20%20dx+%20%5c(%20{%5clambda}Q%20%20%5c)%20%20dy=0}) ・・・・・・(2)
・・・・・・(2)
(2)が完全微分方程式であるためには
%20%20=%5cfrac{%5chspace{2}{%5cpartial}%5chspace{2}}{%5chspace{2}%20{%5cpartial}y%20%20%5chspace{2}}%20%5c(%20{%5clambda}P%20%20%5c)%20%20}) ・・・・・・(3)
・・・・・・(3)
でなければならない.
%20%20})
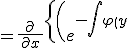%20%20dy%20%20%20%20}%20%20}%20%20%5c)%20%20Q%20%20%5c}%20%20})
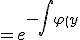%20%20dy%20%20%20%20}%20%20}%5cfrac{%5chspace{2}{%5cpartial}%5chspace{2}}{%5chspace{2}%20{%5cpartial}x%20%20%5chspace{2}}Q})
 ・・・・・・(4)
・・・・・・(4)
%20%20})
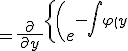%20%20dy%20%20%20%20}%20%20}%20%20%5c)%20%20P%20%20%5c}%20%20})
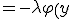%20%20P+{%5clambda}%5chspace{1}{P}_{y}})
%20%20=%5cfrac{%5chspace{2}%20%5chspace{1}{P}_{y}-%20%5chspace{1}{Q}_{x}%20%20%5chspace{2}}{%5chspace{2}P%5chspace{2}}}) を代入すると
を代入すると
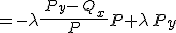
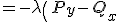%20%20+{%5clambda}%5chspace{1}{P}_{y}})
 ・・・・・・(5)
・・・・・・(5)
(4),(5)より(3)を満足している.
よって
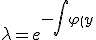%20%20dy%20%20%20%20}%20%20}})
は積分因子である.
ホーム>>カテゴリー分類>>微分>>微分方程式>>積分因子>>積分因子の証明
学生スタッフ作成
最終更新日:
2024年5月17日