2変数関数の極値の証明 (2)
連立方程式%20%20=0,%5chspace{1}{f}_{x}%20%5c(%20a,b%20%20%5c)%20%20=0})
の解%20%20=%20%5c(%20a,b%20%20%5c)%20%20})
に対して
%20%20%5chspace{2}}{%5chspace{2}%20%5chspace{1}{f}_{y}%5cleft({%20a,b%20%20}%5cright)%20%20%5chspace{2}}>%200,%5cleft({%20<%200%20%20}%5cright)%20%20})
ならば
は極小値（極大値）
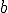
をとる．
■証明
%20%20=0})
によって定められる局所的な関数%20%20})
の極値，つまり陰関数の極値を考える．
で極値%20%20})
をとるとすると
陰関数の微分
より
が極値をもつためには
でなければならない．よって
%20%20%20%20%5chspace{2}}{%5chspace{2}%20%5chspace{1}{f}_{y}%20%5c(%20a,b%20%20%5c)%20%20%20%20%5chspace{2}}=0})
この等式をみたすためには%20%20=0%20%20})
でなければならない．
これを
の式に代入すると
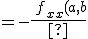%20%20f_{y}^{2}%20%5c(%20a,b%20%20%5c)%20%20%20%20%5chspace{2}}{%5chspace{2}%20f_{y}^{3}%20%5c(%20a,b%20%20%5c)%20%20%20%20%5chspace{2}}%20%20})
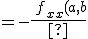%20%20%20%20%5chspace{2}}{%5chspace{2}%20%5chspace{1}{f}_{y}%20%5c(%20a,b%20%20%5c)%20%20%20%20%5chspace{2}}%20%20})
したがって
%20%20%20%20%5chspace{2}}{%5chspace{2}%20%5chspace{1}{f}_{y}%20%5c(%20a,b%20%20%5c)%20%20%20%20%5chspace{2}}>%200})
のとき，極小値
%20%20%20%20%5chspace{2}}{%5chspace{2}%20%5chspace{1}{f}_{y}%20%5c(%20a,b%20%20%5c)%20%20%20%20%5chspace{2}}<%200})
のとき，極大値となる．
ホーム>>カテゴリー別分類>>微分>>偏微分>>2変数関数の極値>>2変数関数の極値の証明 (2)
学生スタッフ作成
最終更新日：
2023年1月21日