$3$\displaystyle{ \frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}} }$ のグラフ

$3$\displaystyle{ \frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}}\text{\hspace{1} } }$ は，反比例の基本形として使われることが多い．

グラフは以下のようになる．

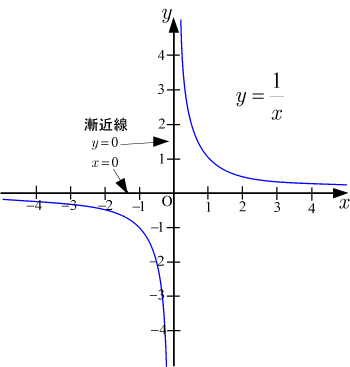
$3$\displaystyle{x=0}$ ， $3$\displaystyle{\text{\hspace{1} }y=0}$ が漸近線である．

■関連動画

■特徴

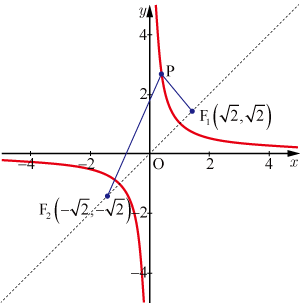
$3$\displaystyle{ y=\frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}} }$ のグラフは， $3$\displaystyle{ \left({ \sqrt{2},\sqrt{2} }\right) }$ ， $3$\displaystyle{ \left({ - \sqrt{2},- \sqrt{2} }\right) }$ が焦点， $3$x$ 軸と $3$y$ 軸が漸近線となる双曲線である．

●確認方法1

関数 $3$\displaystyle{ y=\frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}} }$ のグラフ上の点 $3$\text{P}$ の座標を $3$\displaystyle{\left({ r,s }\right)}$ とする． $3$\displaystyle{s=\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}}}$ より，点 $3$\text{P}$ の座標は， $3$\displaystyle{\left({ r,\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right)}$ と書き換えることができる.

点 $3$\displaystyle{ \left({ \sqrt{2},\sqrt{2} }\right) }$ を点 $3$\displaystyle{\hspace{1}{\text{F}}_{1}}$ ，点 $3$\displaystyle{ \left({ - \sqrt{2},- \sqrt{2} }\right) }$ を点 $3$\displaystyle{\hspace{1}{\text{F}}_{2}}$ とする．

双曲線の定義より

$3$\displaystyle{\left|{ \hspace{1}{\text{F}}_{1}\text{P}- \hspace{1}{\text{F}}_{2}\text{P} }\right|}$ ＝一定　･･････(1)

であれば，関数 $3$\displaystyle{ y=\frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}} }$ のグラフは双曲線である．

$3$\displaystyle{\left|{ \hspace{1}{\text{F}}_{1}\text{P}- \hspace{1}{\text{F}}_{2}\text{P} }\right|}$ $3$\displaystyle{=\left|{ \sqrt{ { \left({ r- \sqrt{2} }\right) }^{2}+{ \left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}}- \sqrt{2} }\right) }^{2} }- \sqrt{ { \left({ r+\sqrt{2} }\right) }^{2}+{ \left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}}+\sqrt{2} }\right) }^{2} } }\right|}$

$3$\displaystyle{=\left|{ \sqrt{ {r}^{2}- 2\sqrt{2}r+2+\frac{\hspace{2}1\hspace{2}}{\hspace{2} {r}^{2} \hspace{2}}- \frac{\hspace{2} 2\sqrt{2} \hspace{2}}{\hspace{2}r\hspace{2}}+2 }- \sqrt{ {r}^{2}+2\sqrt{2}r+2+\frac{\hspace{2}1\hspace{2}}{\hspace{2} {r}^{2} \hspace{2}}+\frac{\hspace{2} 2\sqrt{2} \hspace{2}}{\hspace{2}r\hspace{2}}+2 } }\right|}$

$3$\displaystyle{=\left|{ \sqrt{ {r}^{2}+2+\frac{\hspace{2}1\hspace{2}}{\hspace{2} {r}^{2} \hspace{2}}- 2\sqrt{2}\left({ r+\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right)+2 }- \sqrt{ {r}^{2}+2+\frac{\hspace{2}1\hspace{2}}{\hspace{2} {r}^{2} \hspace{2}}+2\sqrt{2}\left({ r+\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right)+2 } }\right|}$

$3$\displaystyle{=\left|{ \sqrt{ { \left({ r+\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right) }^{2}- 2\sqrt{2}\left({ r+\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right)+2 }- \sqrt{ { \left({ r+\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right) }^{2}+2\sqrt{2}\left({ r+\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right)+2 } }\right|}$

$3$\displaystyle{==\left|{ \sqrt{ { \left{{ \left({ r+\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right)- \sqrt{2} }\right} }^{2} }- \sqrt{ { \left{{ \left({ r+\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right)+\sqrt{2} }\right} }^{2} } }\right|}$

$3$\displaystyle{=\left|{ \left{{ \left({ r+\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right)- \sqrt{2} }\right}- \left{{ \left({ r+\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}} }\right)+\sqrt{2} }\right} }\right|}$

$3$\displaystyle{=\left|{ - 2\sqrt{2} }\right|}$

$3$\displaystyle{=2\sqrt{2}}$ 　･･････(2)

よって，(1)を満たしており， $3$\displaystyle{ y=\frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}} }$ のグラフは双曲線である．

●確認方法2

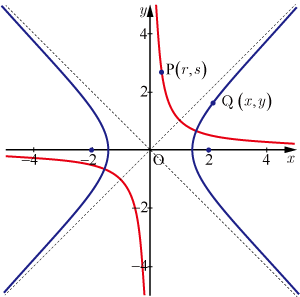
関数 $3$\displaystyle{ y=\frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}} }$ のグラフ上の点 $3$\text{P}$ の座標を $3$\displaystyle{\left({ r,s }\right)}$ とする．関数 $3$\displaystyle{ y=\frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}} }$ のグラフを原点を中心に，時計回りに45°回転させたグラフを青線で示す.点 $3$\text{P}$ が回転により移った先を点 $3$\text{Q}$ とし，その座標を $3$\displaystyle{\left({ x,y }\right)}$ とする．

$3$\left({ x,y }\right)$ と $3$\left({ r,s }\right)$ の関係を回転行列を使って表すと

$3$\displaystyle{\left({ \begin{array}x& \vspace{6}\\ y& \vspace{6}\\ \end{array} }\right)=\left({ \begin{array} \cos \left({ - 45^\circ }\right) & - \sin \left({ - 45^\circ }\right) & \vspace{6}\\ \sin \left({ - 45^\circ }\right) & \cos \left({ - 45^\circ }\right) & \vspace{6}\\ \end{array} }\right)\left({ \begin{array}r& \vspace{6}\\ s& \vspace{6}\\ \end{array} }\right)}$

$3$\displaystyle{\left({ \begin{array}r& \vspace{6}\\ s& \vspace{6}\\ \end{array} }\right)=\left({ \begin{array} \cos 45^\circ & - \sin 45^\circ & \vspace{6}\\ \sin 45^\circ & \cos 45^\circ & \vspace{6}\\ \end{array} }\right)\left({ \begin{array}x& \vspace{6}\\ y& \vspace{6}\\ \end{array} }\right)}$

$3$\displaystyle{=\left({ \begin{array} \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}} & - \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}} & \vspace{6}\\ \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}} & \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}} & \vspace{6}\\ \end{array} }\right)\left({ \begin{array}x& \vspace{6}\\ y& \vspace{6}\\ \end{array} }\right)}$

$3$\displaystyle{=\left({ \begin{array} \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}x- \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}y & \vspace{6}\\ \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}x+\frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}y & \vspace{6}\\ \end{array} }\right)}$

よって

$3$\displaystyle{r=\frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}x- \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}y}$ 　･･････(3)

$3$\displaystyle{s=\frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}x+\frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}y}$ 　･･････(4)

となる．

点 $3$\text{P}$ が関数 $3$\displaystyle{ y=\frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}} }$ のグラフ上の点より

$3$\displaystyle{s=\frac{\hspace{2}1\hspace{2}}{\hspace{2}r\hspace{2}}}$ 　･･････(5)

の関係がある.(5)に(4)，(3)を代入すし，整理する．

$3$\displaystyle{\frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}x+\frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}y=\frac{\hspace{2}1\hspace{2}}{\hspace{2} \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}x- \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}y \hspace{2}}}$

$3$\displaystyle{\left({ \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}x+\frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}y }\right)\left({ \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}x- \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}y }\right)=1}$

$3$\displaystyle{{\left({ \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}x }\right)}^{2}- {\left({ \frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2}2\hspace{2}}y }\right)}^{2}=1}$

$3$\displaystyle{\frac{\hspace{2} {x}^{2} \hspace{2}}{\hspace{2} { \left({ \sqrt{2} }\right) }^{2} \hspace{2}}- \frac{\hspace{2} {y}^{2} \hspace{2}}{\hspace{2} { \left({ \sqrt{2} }\right) }^{2} \hspace{2}}=1}$ 　･･････(6)

の関係がえられる．この方程式は，双曲線の方程式になっていおり，青線は双曲線であることが分かる．したがって，回転移動させる前のグラフも双曲線になる．

ホーム>>カテゴリー分類>>関数>> $3$\displaystyle{ \frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}} }$ のグラフ

学生スタッフ作成
最終更新日： 2025年5月14日