余弦定理

三角形の各辺 $3$\displaystyle{a}$ , $3$\displaystyle{b}$ , $3$\displaystyle{c}$ と各角 $3$\displaystyle{\text{A}}$ , $3$\displaystyle{\text{B}}$ , $3$\displaystyle{\text{C}}$ の間には以下に示す関係がある．

$3$\begin{array}{lll}{a}^{2}={b}^{2}+{c}^{2}- 2bc\cos \text{A}& \vspace{6}\\ {b}^{2}={c}^{2}+{a}^{2}- 2ca\cos \text{B}& \vspace{6}\\ {c}^{2}={a}^{2}+{b}^{2}- 2ab\cos \text{C}& \vspace{6}\\ \end{array}$

この関係を余弦定理という．

■証明

三角形の頂点 $3$\displaystyle{\text{C}}$ から辺 $3$\displaystyle{\text{AB}}$ に垂線 $3$\displaystyle{\text{CD}}$ を引く．
直角三角形 $3$\displaystyle{\text{ACD}}$ と直角三角形 $3$\displaystyle{\text{BCD}}$ ができる．
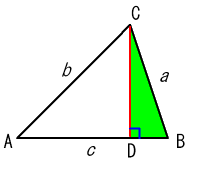直角三角形 $3$\displaystyle{\text{BCD}}$ に三平方の定理を用いると

$3${\text{CB}}^{2}={\text{CD}}^{2}+{\text{BD}}^{2}$ ･･････(1)

となる．

$3$\displaystyle{ \text{CB}=a }$ ， $3$\displaystyle{ \text{CD}=b\sin \text{A} }$ (⇒ここを参照)， $3$\displaystyle{ \text{BD}=c- b\cos \text{A} }$ の関係を(1)に代入すると

$3$\begin{array}{lll}{a}^{2}={ $ b\sin \text{A} $ }^{2}+{ $ c- b\cos \text{A} $ }^{2}& \vspace{6}\\ \text{\hspace{10} }={b}^{2}{\sin }^{2}\text{A}+{c}^{2}- 2cb\cos \text{A}+{b}^{2}{\cos }^{2}\text{A}& \vspace{6}\\ \text{\hspace{10} }={b}^{2} $ { \sin }^{2}\text{A}+{ \cos }^{2}\text{A} $ +{c}^{2}- 2cb\cos \text{A}& \vspace{6}\\ \text{\hspace{10} }={b}^{2}+{c}^{2}- 2bc\cos \text{A}& \vspace{6}\\ {}_\bullet\limits{ }^\bullet {}_\bullet {a}^{2}={b}^{2}+{c}^{2}- 2bc\cos \text{A}& \vspace{6}\\ \end{array}$

が求められる．

$3$\displaystyle{ \text{A}=90^\circ }$ ，鈍角の場合の証明は省略

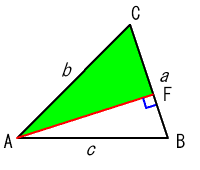
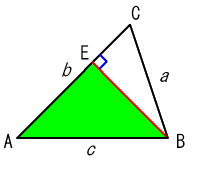同様にして，

$3$\begin{array}{b}^{2}={c}^{2}+{a}^{2}- 2ca\cos \text{B}& \vspace{6}\\ {c}^{2}={a}^{2}+{b}^{2}- 2ab\cos \text{C}& \vspace{6}\\ \end{array}$

も求められる．

■内積を用いた証明

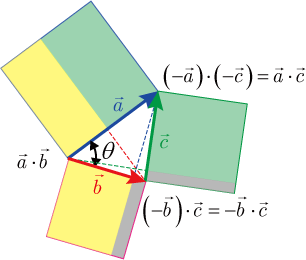
図より(図を理解するには内積の幾何学的検討のページが参考になる)

$3$\displaystyle{{c}\limits^{\rightarrow }={a}\limits^{\rightarrow }- {b}\limits^{\rightarrow }}$ 　･･････(2)

両辺のベクトルの大きさも等しくなるので

$3$\displaystyle{\left|{{c}\limits^{\rightarrow }}\right|=\left|{ {a}\limits^{\rightarrow }- {b}\limits^{\rightarrow } }\right|}$ 　･･････(3)

(3)の両辺を2乗する．

$3$\displaystyle{{\left|{{c}\limits^{\rightarrow }}\right|}^{2}={\left|{ {a}\limits^{\rightarrow }- {b}\limits^{\rightarrow } }\right|}^{2}}$ 　･･････(4)

内積の計算則を使って，(4)の右辺を以下のように式変形をする．

$3$\displaystyle{{\left|{{c}\limits^{\rightarrow }}\right|}^{2}=\left({ {a}\limits^{\rightarrow }- {b}\limits^{\rightarrow } }\right)\cdot \left({ {a}\limits^{\rightarrow }- {b}\limits^{\rightarrow } }\right)}$

$3$\displaystyle{=\left({ {a}\limits^{\rightarrow }- {b}\limits^{\rightarrow } }\right)\cdot {a}\limits^{\rightarrow }+\left({ {a}\limits^{\rightarrow }- {b}\limits^{\rightarrow } }\right)\cdot \left({ - {b}\limits^{\rightarrow } }\right)}$

$3$\displaystyle{=\left({ {a}\limits^{\rightarrow }- {b}\limits^{\rightarrow } }\right)\cdot {a}\limits^{\rightarrow }- \left({ {a}\limits^{\rightarrow }- {b}\limits^{\rightarrow } }\right)\cdot {b}\limits^{\rightarrow }}$

$3$\displaystyle{={a}\limits^{\rightarrow }\cdot {a}\limits^{\rightarrow }- {b}\limits^{\rightarrow }\cdot {a}\limits^{\rightarrow }- {a}\limits^{\rightarrow }\cdot {b}\limits^{\rightarrow }+{b}\limits^{\rightarrow }\cdot {b}\limits^{\rightarrow }}$

$3$\displaystyle{={\left|{{a}\limits^{\rightarrow }}\right|}^{2}+{\left|{{b}\limits^{\rightarrow }}\right|}^{2}- 2{a}\limits^{\rightarrow }\cdot {b}\limits^{\rightarrow }}$

$3$\displaystyle{={\left|{{a}\limits^{\rightarrow }}\right|}^{2}+{\left|{{b}\limits^{\rightarrow }}\right|}^{2}- 2\left|{{a}\limits^{\rightarrow }}\right|\left|{{b}\limits^{\rightarrow }}\right|\cos {\theta}}$

ここで

$3$\displaystyle{\left|{{a}\limits^{\rightarrow }}\right|=a}$ ， $3$\displaystyle{\left|{{b}\limits^{\rightarrow }}\right|=b}$ ， $3$\displaystyle{\left|{{c}\limits^{\rightarrow }}\right|=c}$ とおくと

$3$\displaystyle{{c}^{2}={a}^{2}+{b}^{2}- 2ab\cos {\theta}}$

となり，余弦定理が導かれた．

ホーム>>カテゴリー分類>>三角関数>>余弦定理

最終更新日： 2023年10月26日