平面の極座標（円座標）

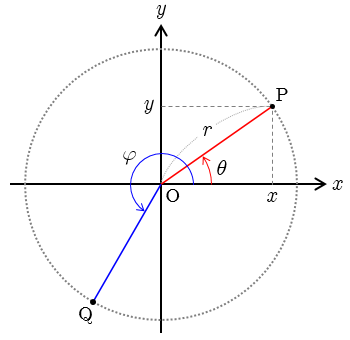
2次元平面において，動径座標 $3$\displaystyle{r}$ と角度座標 $3$\displaystyle{{\theta}}$ を用いて任意の点の位置を指定するとき， $3$\displaystyle{ $r,{\theta}$ }$ を平面の極座標もしくは円座標という．

図のように，平面の直交座標において，原点 $3$\displaystyle{\text{O}}$ から点 $3$\displaystyle{\text{P}}$ までの動径の距離を $3$\displaystyle{r}$ ， $3$\displaystyle{+x}$ 軸から測った動径の角度を $3$\displaystyle{{\theta}}$ とすると，平面の極座標 $3$\displaystyle{ $r,{\theta}$ }$ と平面の直交座標 $3$\displaystyle{ $x,y$ }$ との間には

$3$\displaystyle{ x=r\cos {\theta} }$ - - - (1)
$3$\displaystyle{ y=r\sin {\theta} }$ - - - (2)

の関係がある．

$3$\displaystyle{ 0\leq r< \infty }$ 及び $3$\displaystyle{ - {\pi}< {\theta}\leq {\pi} }$ の範囲を考えると，平面上の任意の点を一意的に指定できるが，原点 $3$\displaystyle{ $x,y$=$0,0$ }$ は角度が定まらず特異点 $3$\displaystyle{ $r,{\theta}$=$0,{\theta}$ }$ となる．また， $3$\displaystyle{ - {\pi}< {\theta}\leq {\pi} }$ の場合には，平面の直交座標から平面の極座標への変換が

$3$\displaystyle{ r=\sqrt{ {x}^{2}+{y}^{2} } }$ - - - (3)
$3$\displaystyle{ {\theta}=sgn$y${\cos }^{ - 1 } $ \frac{\hspace{2}x\hspace{2}}{\hspace{2} \sqrt{ {x}^{2}+{y}^{2} } \hspace{2}} $ }$ - - - (4)

で与えられる．式(4)における $3$\displaystyle{sgn}$ は以下に示す符号関数である（ $3$\displaystyle{y\geq 0}$ ならプラス， $3$\displaystyle{y< 0}$ ならマイナスの符号がつく）：

$3$\displaystyle{ sgn$y$=\left{{ \begin{array}1& $y\geq 0$ & \vspace{6}\\ - 1 & $y< 0$ & \vspace{6}\\ \end{array} }$

ただし，原点は特異点であり，式(4)の逆余弦関数において分母がゼロとなるため角度が定義できない．

ホーム>>カテゴリー分類>>その他>>座標系>>平面の極座標（円座標）