2元1次連立方程式の解についての平面座標を用いた考察
2元1次連立方程式
・・・・・・(1)
を行列を使って表わすと
・・・・・・(2)
となる.また係数行列
の列ベクトル
,を使って表わすと
・・・・・・(3)
となる.
,
,
とおくと,(3)は
・・・・・・(4)
と表わされる.(4)の関係を
平面において幾何学的に表現すると下図のようになる:
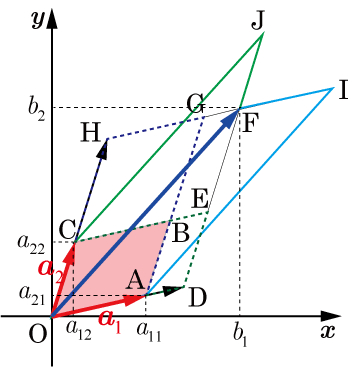
(
,
,
より,(4)は
と表現される.)
この図より
ベクトル
,
を2辺とする平行四辺形
の面積を
,
ベクトル
,
を2辺とする平行四辺形
の面積を
,
ベクトル
,
を2辺とする平行四辺形
の面積を
,
ベクトル
,
を2辺とする平行四辺形
の面積を
,
ベクトル
,
を2辺とする平行四辺形
の面積を
,
と定めると,
,
である.ここで
,
であるので
,
となる.よって,
,
は面積比となっている.
平行四辺形の面積は行列式を使って求めることができ(※),
となる.したがって
,
が得られる.これらの解を表わす式はクラメルの公式になっている.
ホーム>>カテゴリー分類>>行列>>線形代数>>2元1次連立方程式の解についての平面座標を用いた考察
最終更新日:
2023年12月4日
