三角関数の合成公式
■ sin(正弦)での合成
 ・・・・・・(1)
・・・・・・(1)
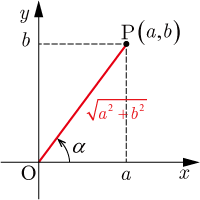
ただし,はの係数を成分,の係数を成分とする点
と原点
を結ぶ線分
と
軸のなす角を一般角で表したものである.
(1)が成り立つとすると
,
となる.いいかえると,
は
,
を満たす.図はこの関係を示したものである.通常,
とする.
⇒公式の導出,ベクトルを用いた三角関数の合成公式の導出
■ cos(余弦)での合成
 ・・・・・・(2)
・・・・・・(2)
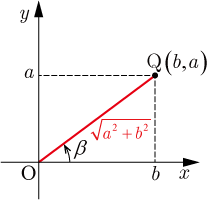
ただし,はの係数を成分,の係数を成分とする点
と原点
を結ぶ線分
と 軸のなす角を一般角で表したものである.
(2)が成り立つとすると
,
となる.いいかえると,
は
,
を満たす.図はこの関係を示したものである.通常,
とする.
⇒公式の導出,ベクトルを用いた三角関数の合成公式の導出
■解説動画
■関連動画
■公式の導出
●sinでの合成:
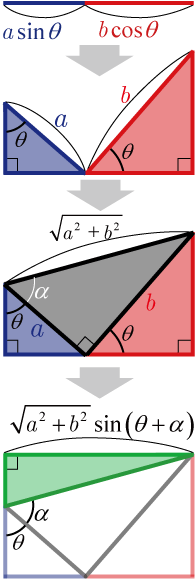 ,, の場合,図より合成公式が導かれる.
,, の場合,図より合成公式が導かれる.
次に, あるいは において式を変形して合成の公式を導く.
,とおくと
( 加法定理より)
【参考】
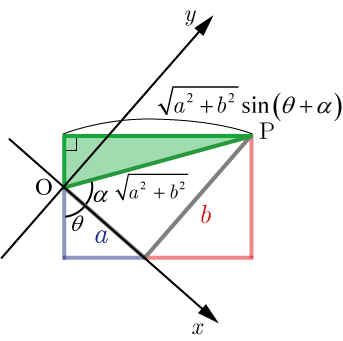
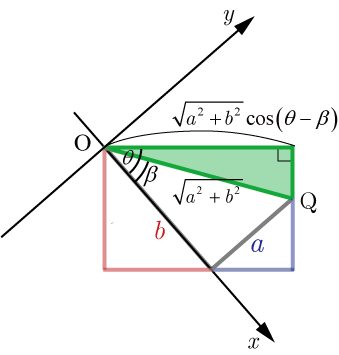
●cosでの合成:
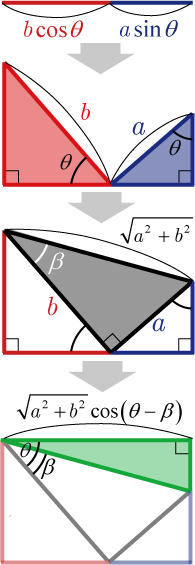 ,
,
の場合,図より合成公式が導かれる.
,
,
の場合,図より合成公式が導かれる.
次に,
あるいは
において式を変形して合成の公式を導く.
,とおくと
(
加法定理より)
ホーム>>カテゴリー分類>>三角関数>>合成公式
最終更新日:
2025年6月30日
 ・・・・・・(1)
・・・・・・(1)
 ・・・・・・(2)
・・・・・・(2) ,, の場合,図より合成公式が導かれる.
,, の場合,図より合成公式が導かれる. 
 ,
,
の場合,図より合成公式が導かれる.
,
,
の場合,図より合成公式が導かれる. 