ベクトルを用いた三角関数の合成公式の導出
・sin(正弦)での合成
・cos(余弦)での合成
■証明
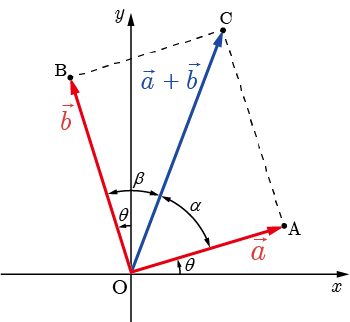 図のように
と
を定める.ただし,
,とする.
図のように
と
を定める.ただし,
,とする.
各ベクトルを成分表示すると
・・・・・・(1)
・・・・・・(2)
である.
,
,
の終点をそれぞれ
点,
点,
点とする.
と
のなす角は
であるので,
は直角三角形である.よって,
は
三平方の定理より
となる.と
軸のなす角は
である.よって
を成分表示すると
・・・・・・(3)
となる.また,と
軸のなす角は
である.よってを使って
を成分表示すると
・・・・・・(4)
となる.
一方,(1),(2)より
・・・・・・(5)
となる.(3),(4),(5)の成分は等しい.よって
ただし,
,
が得られる.
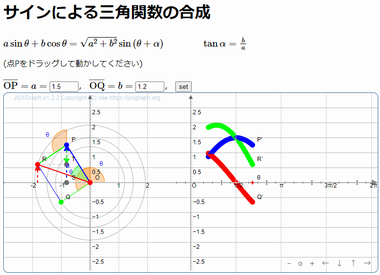
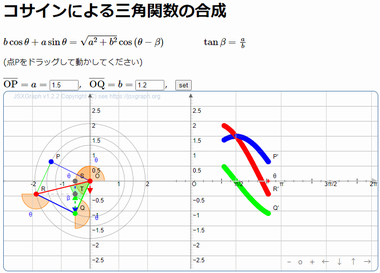
■インターラクティブなグラフ
下の画像をクリック
ホーム>>カテゴリー分類>>三角関数>>合成公式
最終更新日:
2024年9月8日
 図のように
と
を定める.ただし,
,とする.
図のように
と
を定める.ただし,
,とする.

