ベクトルを用いた加法定理の証明
(複号同順)
■証明
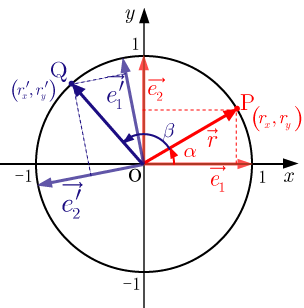 軸の正方向の基本ベクトルを
,軸の正方向の基本ベクトルを ,単位円上の点Pの位置ベクトルをとする.
軸の正方向の基本ベクトルを
,軸の正方向の基本ベクトルを ,単位円上の点Pの位置ベクトルをとする.
を成分表示すると
・・・・・・(1)
と表されるとする.ただし,三角関数の定義より
・・・・・・(2)
・・・・・・(3)
となる.
軸の正方向の基本ベクトルを ,軸の正方向の基本ベクトルをとすると,の基本ベクトル表示は
・・・・・・(4)
ここで,,
, を原点を中心に角度
だけ半時計回りに回転させたものをそれぞれ,
,
,とすると,それぞれのベクトルの位置関係は変わらないので
・・・・・・(5)
の関係が得られる.
, を成分表示で表すと
・・・・・・(6)
(三角関数の計算の基礎を参照) ・・・・・・(7)
となる.
(6),(7)を(5)に代入すると
・・・・・・(8)
となる.
一方,と軸のなす角は
であるので,を成分表示で表すと
・・・・・・(9)
となる.
(8)と(9)は同じを成分表示したものであるので,そてぞれの成分はお互いに等しい.よって
・・・・・・(10)
・・・・・・(11)
となる.
以上より加法定理が導かれた.
ホーム>>カテゴリー分類>>三角関数>>加法定理>>加法定理の証明(ベクトル編)
最終更新日
2023年3月2日
 軸の正方向の基本ベクトルを
,軸の正方向の基本ベクトルを ,単位円上の点Pの位置ベクトルをとする.
軸の正方向の基本ベクトルを
,軸の正方向の基本ベクトルを ,単位円上の点Pの位置ベクトルをとする.