行列式の幾何学的意味

平面上のベクトル $a = (\begin{matrix} x_{1} \\ y_{1} \end{matrix})$ ， $b = (\begin{matrix} x_{2} \\ y_{2} \end{matrix})$ を2辺とする平行四辺形の面積 $S$ は，それらのベクトルの成分を各列の成分とする行列 $(\begin{matrix} x_{1} & x_{2} \\ y_{1} & y_{2} \end{matrix})$ の行列式の値の絶対値に等しい．

■導出

$x y$ 平面上のベクトル $a$ ， $b$ を

$a = (\begin{matrix} x_{1} \\ y_{1} \end{matrix})$ ， $b = (\begin{matrix} x_{2} \\ y_{2} \end{matrix})$

とおく． $x$ 軸とのなす角を $α, β$ とすると，2つのベクトルの作る平行四辺形の面積 $S$ は

$S = ||a| |b| \sin (β - α)|$

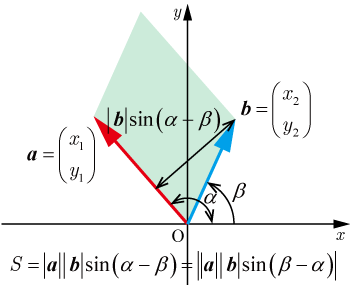
加法定理を使って式変形をする

$= ||a| |b| (\sin β \cos α - \cos β \sin α)|$

$= ||a| |b| \sin β \cos α - |a| |b| \cos β \sin α|$

$= ||a| \cos α |b| \sin β - |a| \sin α |b| \cos β|$ ･･････(1)

となる．絶対値をとっているのは， $α$ と $β$ の値によっては $\sin (β - α)$ 値が負になる場合もあるからである．

ここで， $a$ ， $b$ のベクトル成分は

$x_{1} = |a| \cos α$

$y_{1} = |a| \sin α$

$x_{2} = |b| \cos β$

$y_{2} = |b| \sin β$

で表せるから，それぞれ(1)式に代入すると

$S = |x_{1} y_{2} - y_{1} x_{2}|$ ･･････(2)

が得られる．

次に， $a = (\begin{matrix} x_{1} \\ y_{1} \end{matrix})$ の成分を第1列の成分， $b = (\begin{matrix} x_{2} \\ y_{2} \end{matrix})$ の成分を第2列の成分とする行列 $(\begin{matrix} x_{1} & x_{2} \\ y_{1} & y_{2} \end{matrix})$ の行列式の値をを計算すると

$| \begin{matrix} x_{1} & x_{2} \\ y_{1} & y_{2} \end{matrix} | = x_{1} y_{2} - y_{1} x_{2}$ ･･････(3)

となる．

よって，ベクトル $a$ ， $b$ を2辺とする平行四辺形の面積 $S$ は，それらのベクトルの成分を各列の成分とする行列の行列式の値の絶対値に等しい．

ここで，注意しなければならないのはベクトル $a$ ， $b$ の位置関係によって行列式の値が負になる場合があるので，面積を求める場合は行列式の値の絶対値をとっている．

ホーム>>カテゴリー別分類>>積分>>重積分>>行列式の幾何学的意味

学生スタッフ作成
最終更新日： 2026年1月20日