概念問題 解答

高校数学　数学II

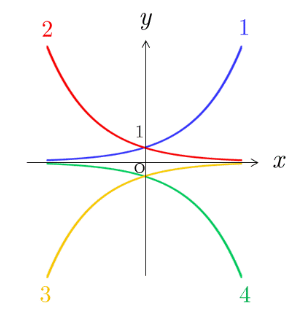
問題2の解答

指数関数 ${\displaystyle y=-2^{-x}}$ の基本となる関数は

${\displaystyle y=2^x}$

である底が2で1より大きい．よって， $x$ が増加すると$y$も増加する増加関数である．グラフは図の1になる．

${\displaystyle 2^{-x}=2^{-1\cdot x}=2^{x\cdot \left(-1\right)}={\left(2^x\right)}^{-1}=\frac{1}{2^x}}$ より（指数計算の基本を参照）

のように式変形できる．

${\displaystyle \frac{1}{2^x}}$ は分母が増加関数なので，${\displaystyle \frac{1}{2^x}}$ は，$x$ が増加すると0に近づいていく．

${\displaystyle -\frac{1}{2^x}}$ は${\displaystyle \frac{1}{2^x}}$に${\displaystyle -1}$ を掛けたものになるので，負の値で， $x$ が増加すると0に近づいていくことになる．

上記のようなグラフが答えである．

以上より，答えは3となる．

■別解

${\displaystyle y=-2^{-x}}$ 　→　${\displaystyle -y=2^{-x}}$

と書きかえる．

${\displaystyle y=-2^{-x}}$ のブラフは，${\displaystyle y=2^x}$ のブラフを原点に関して対称移動したものである．

なぜなら，${\displaystyle \left(x,y\right)\to \left(-x,-y\right)}$ に置き換わっている．

${\displaystyle y=2^x}$ のブラフは1のブラフに対応するので， ${\displaystyle -y=2^{-x}}$ のグラフは3になる．