減衰振動 ： ばね‐質量‐ダンパー系 (spring - mass - damper system)

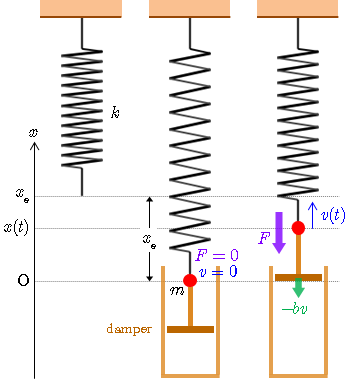
ばねの先端に取り付けられたおもりにダンパー（制動器）を取り付けた系（ばね‐質量系にダンパーを加えた系：ばね‐質量‐ダンパー系）の運動を考える．ダンパーはおもりの運動を抑制する抵抗力をおもりに加える役割を果たす．

このばね‐質量‐ダンパー系の数学モデルを得るために以下を仮定する：

• 重力加速度の大きさ g は一定である．
• おもりは質量 m の質点である．
• ばねの質量およびダンパーの可動部の質量はゼロである（おもりと可動部の質量を合わせて m としてもよい）．
• ばねは常にフックの法則に従い，その弾性定数（ばね定数）を k (>0) とする．
• ダンパーはおもりの速度に比例した抵抗力をおもりに作用させ，その比例定数を b (>0) とする．
• 空気の影響は無い（おもりの速度に比例する空気抵抗（流体の抵抗）を考えて，空気（流体）がダンパーの役割を果たすとしてもよいが，ここでは制動器のみの抵抗を考える）．

図のように，質量 m の質点（赤丸）を先端に付けたばねを鉛直に吊るし，質点にはダンパーを取り付ける．質点を静止させたとき，ばねは自然長から xe だけ伸びたとすると，質点に抵抗力は作用せず，鉛直上向きの弾性力 kxe と下向きの重力 mg が釣り合い， kxe −mg =0 が成り立つ．この釣り合いの位置を原点 O として鉛直上向きに x 軸をとる．

質点を振動させたときに質点に作用する力は，質点の位置 x と速度 v を用いて，

ばねの弾性力 ：  −k ( x−xe )
ダンパーによる抵抗力 ：  −bv   （ b ：正の比例定数）
重力 ：  −mg

と表されるので，それらの合力 F は

F= −k( x−xe ) −bv −mg =−kx −bv +kxe −mg =−kx −bv     - - - (1)

である（釣り合いの位置を原点 O にとると，重力の影響は考慮しなくてよい）．したがって，質点の運動方程式は

m d2 x dt2 =−kx −bv     - - - (2)

となる．上式の両辺を m で割り，減衰率 γ= b2m ，単振動の角振動数 ω0= km  を導入して整理すると，式(2)は

d2x dt2 +2γ dx dt + ω02x =0     - - - (3)

と表され，減衰振動の従う微分方程式が得られる．この微分方程式を解くと， γ と ω0 の関係に応じて，不足減衰（ γ< ω0 ），臨界減衰（ γ= ω0 ），過減衰（ γ> ω0 ）の解が求まる．

ばね‐質量‐ダンパー系のシミュレーションにより，これらの解が確認できる．

ホーム>>カテゴリー分類>>力学>>質点の力学>>減衰振動>>ばね‐質量‐ダンパー系