単振り子：周期の厳密解 (excact solution of period)

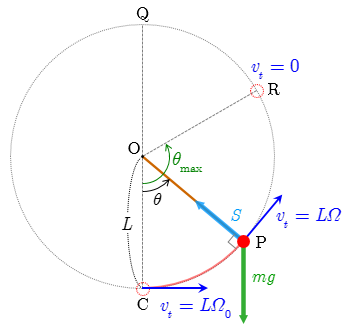
鉛直面内で回転運動できるように点 O で固定した軽い棒の先端に質量 m の質点を取り付けた単振り子について，点 O から引いた鉛直軸 OC と棒とのなす角を θ とする（反時計回りに回転する角の向きを正にとる）．

単振り子の角速度 Ω= dθdt を用いて，速度の接線方向成分を vt= Ldθdt =LΩ と表し，最下点 C での角速度の大きさを Ω0 とする．力学的エネルギー保存則より，最下点 C での運動エネルギーが最高点 Q と最下点 C との間の重力による位置エネルギーの差よりも小さい場合，つまり

12 m ( LΩ0 ) 2 <2mgL ⇒ Ω0 <2 gL --- (1)

の場合，単振り子は往復運動となり，大きい場合

Ω0 >2 gL --- (2)

において，一方向に回る回転運動となる．また，等しい場合

Ω0 =2 gL --- (3)

では，最高点 Q で速さが 0 になり静止する．ここで

k= Ω0 2 Lg --- (4)

とおくと，式 (1) の場合は k<1 であり，式 (2) の場合は k>1 となる．各々の場合において，単振り子の周期 T は以下のように表される（式 (3) の場合 ( k=1 )，振り子は最高点 Q で静止するので周期は存在しない）．

◆ 往復運動の場合 k<1

T=4 Lg K(k) --- (5) ⇒ 導出

ここで， K(k) は第1種の完全楕円積分であり，次式で与えられる．

K(k) = ∫0 π/2 dφ 1− k2 sin2 φ --- (6)

Ω0 が非常に小さい微小振動（ k≪1 ）の場合，上式において

1−k2 sin2φ ≈1 --- (7)

と近似できるので，第1種の完全楕円積分の値は K(k) ≈ ∫0 π/2 dφ =π2 となる．したがって，周期は T=4 L/g ⋅ π2 =2π L/g となり，近似解における周期と一致する．

次に， k は小さいが無視できないとき，つまり，式 (7) のように近似できない場合を考える．式 (6) を k2 sin2φ に関して展開し，単振り子の最大の振れ角を θmax として，力学的エネルギー保存則から得られる関係式 k2 = sin2 θmax 2 を用いると，式 (5) は

T =2π Lg { 1+ (12) 2 sin2 θmax 2 + ( 1⋅3 2⋅4 ) 2 ( sin2 θmax 2 ) 2 + ( 1⋅3⋅5 2⋅4⋅6 ) 2 ( sin2 θmax 2 ) 3 +⋯ } --- (8)

のように展開できる（詳細）．したがって， θmax が小さい場合は最初の数項だけ考慮すればよい． sin θmax 2 ≈ θmax 2 と近似できるくらいの小さな振動では，式 (8) の第2項目までとって

T ≈2π Lg ( 1+ θmax2 16 ) --- (9)

と表せば十分である．

◆ 回転運動の場合 k>1

この場合，円周を1回転する時間が周期 T となり，第1種の完全楕円積分を用いて次式で表される．

T=2k Lg K (1/k) --- (10) ⇒ 導出

k が大きい場合は， κ=1/k とおいて，式 (10) を

T =2 Lg { κ+ (12) 2 κ3 + ( 1⋅3 2⋅4 ) 2 κ5 + ( 1⋅3⋅5 2⋅4⋅6 ) 2 κ7 +⋯ } --- (11)

のように展開し，最初の数項だけ考慮すればよい（詳細）．

◆ 往復運動も回転運動もしない場合 k=1

この場合，質点が最下点 C ( θ=0 ) から角 θ の位置に到達するまでにかかる時間 t(θ) は次式で表される．

t(θ) = Lg tanh −1 ( sinθ2 ) --- (12) ⇒ 導出

式 (12) において， θ→π の極限を考えると， lim θ→π sinθ2 = sinπ2 =1 より

lim θ→π t(θ) = Lg limx→1 tanh−1 x=∞

となる．つまり，質点が最高点 Q ( θ=π ) に達するには無限の時間がかかることになる．したがって，厳密には，質点は最高点 Q には限りなく近づいていくが，質点の速さは 0 に限りなく近づいていき，最高点 Q に到達することが出来ない．

単振り子 ： 周期の厳密解 (excact solution of period)