単振り子 ： 近似解 (approximate solution)
半径
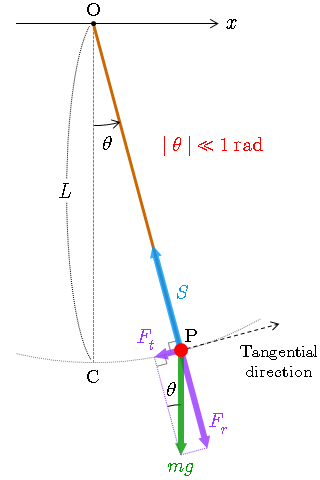
L
の円弧上を質量
m
の質点が往復運動する単振り子について，円の接線方向における質点の運動方程式は
mL
d2θ
dt2
=
−mgsinθ
- - - (1)
と表される（導出）．両辺を
mL
で割って整理すると，
d2θ
dt2
+gLsinθ
=0
- - - (2)
が得られる．単振り子の往復運動において，振れ幅が十分に小さい場合，つまり
|θ|
≪
1 rad
の場合，近似的に
sinθ≈θ
とおくことができるので，式 (2) は
d2θ
dt2
+gLθ
=0
- - - (3)
となる．上式は定数係数の2階同次線形微分方程式であり，単振動の従う微分方程式の標準形と同じ形をしている．ここで，
ω=
gL
- - - (4)
とおいて，この微分方程式を解くと，一般解として，
θ(t)
=
θmaxcos
(
ωt+α
)
- - - (5)
が得られる．したがって，角
θ
は，角振動数
ω=
g/L
，振幅
θmax
，初期位相
α
で単振動する．一般解において，
θmax
，
α
は任意定数であり，初期条件を満たすように決定される．
この近似解では，単振り子の1往復にかかる時間は，式 (5) で表される単振動の周期であるので，その周期
T
は
T=
2πω
=
2π
Lg
- - - (6)
となる．棒（または糸）の長さ
L
が長いほど単振り子の周期は長くなるが，この近似解の場合，周期
T
は質点の質量
m
や振幅
θmax
には依存しない．このように単振り子の振動周期が振れ幅の大きさに関係なく一定であることを，振り子の 等時性 (isochronism) という．また，単振り子の振動数
f
は次式で表される．
f=1T
=12π
gL
- - - (7)
単振り子の鉛直面に沿って水平方向に
x
軸をとると，質点の位置の水平方向成分は，
x=Lsinθ
で表されるが，単振り子の振れ幅が十分に小さい場合，
sinθ≈θ
なので
x(t)
≈L
θ(t)
=L
θmaxcos
(
ωt+α
)
- - - (8)
と近似できる（
θmax
≪
1 rad
）．よって，質点の位置に関しても単振動であるといえる．
例として，長さ
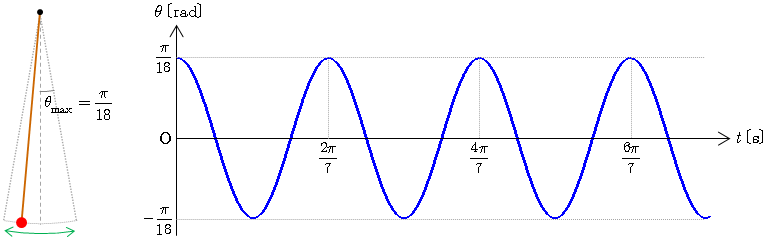
20 cm
の糸に質量
100 g
の小球を取り付けた単振り子について，時刻
t=0
で糸を緩まないように張ったまま鉛直軸から
10°
の角度のところまで質点を持ち上げ静かに放した場合を考える．
10°
=π/18
は
1 rad
に比べて十分小さいとは言えないが，近似解にあてはめると，
g=9.8
m/s2
，
L=0.20 m
より
ω=
gL
=
9.80.20
=
49
=7.0
s-1
なので，
θ=
θmaxcos
(
7.0t+α
)
となる．角速度は
dθ/dt
=−7.0
θmaxsin
(
7.0t+α
)
となり，初期条件より
θmaxcosα
=π18
，
7.0θmaxsinα
=0
を満たすのは，
θmax
=π/18
，
α=0
である．したがって，このときの角
θ
の近似解は
θ(t)=
(π/18)
cos7.0t
である．周期は
T=
2π/ω
=2π/7.0
〔s〕
となる（近似解のシミュレーション）．
ホーム>>カテゴリー分類>>力学>>質点の力学>>単振り子>>近似解
最終更新日：2022年12月20日