単振り子 (simple pendulum)

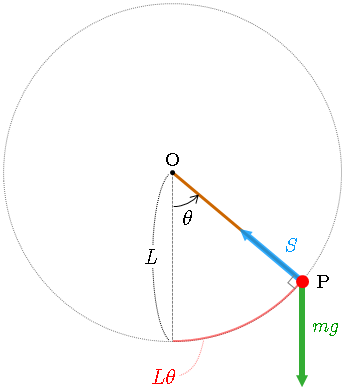
伸縮しない棒の一端を，一つの鉛直面内で回転運動できるように固定し，他端におもりを取り付け，その鉛直面内で運動させたものを単振り子 (simple pendulum) という．ここで，以下を仮定している：

重力加速度の大きさ g は一定である．
おもりは質量 m の質点である．
棒の長さは L で，質量はゼロである（無視できる）．
棒の一端を固定している点で摩擦はなく，滑らかに回転できる．
空気の影響は無い．

図に示すように，棒の一端の位置は点 O に固定され，おもりの位置を点 P ，棒が鉛直方向となす角を θ とする．おもりには鉛直下方に大きさ mg の重力と動径方向（円の法線方向）に棒からの力 S （P から O の向きを正とする）が作用する．

棒がおもりを点 O の向きへ引っ張る ⇒ S>0
棒がおもりを点 O から外向きに押す ⇒ S<0

棒からの力 S により，おもりの運動は半径 L の円周上に束縛される．単振り子の運動において，常に S>0 であれば，棒を伸縮しない糸で置き換えることができる（糸はおもりを押せない）．

単振り子の振れ幅が小さければ（角 θ が微小），その運動は近似的に単振動とみなせる（近似解）．このとき，角 θ は

θ(t) = θmax cos(ωt+α) - - - (1)

と表され， ω= g/L はこの単振動の角振動数はであり， θmax は振れ角の最大値（角 θ の振幅）， α は初期位相を表す．したがって，単振り子が単振動とみなせる場合の周期 T は

T= 2πω = 2π Lg - - - (2)

と表される．この場合，周期 T は振幅 θmax に関係なく一定であり，これを振り子の等時性 (isochronism) という．すなわち，棒（糸）の長さがおなじであれば，振り子が大きく振れても小さく振れても，往復にかかる時間は同じということである（この法則はガリレオ・ガリレイが発見し，そのときガリレオは19歳の学生であった）．

単振り子は一つの鉛直面内だけでの運動であるが，振り子のおもりが一つの鉛直面内だけではなく球面上を運動する場合，その振り子を球面振り子 (spherical pendulum) という．

ホーム>>カテゴリー分類>>力学>>質点の力学>>単振り子

最終更新日：2022年12月20日