水平ばね振り子
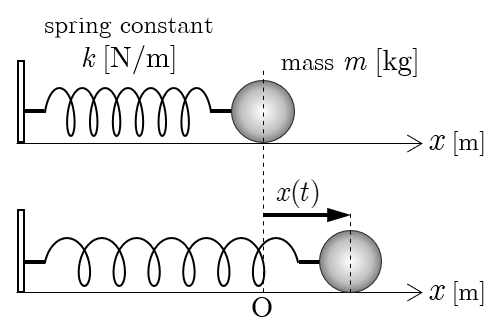 図のように,水平な滑らかな床の上で,軽いばねの一端を壁に固定して,他端に質量
の物体をつけて,ばねを水平方向に自然長から
伸ばしてから静かに放すと単振動を始めた.ここで,ばねはフックの法則に従うものとし,ばね定数を
として,
軸の正の向きを水平方向の右向き,ばねが自然長のときの物体の位置を原点とする.
図のように,水平な滑らかな床の上で,軽いばねの一端を壁に固定して,他端に質量
の物体をつけて,ばねを水平方向に自然長から
伸ばしてから静かに放すと単振動を始めた.ここで,ばねはフックの法則に従うものとし,ばね定数を
として,
軸の正の向きを水平方向の右向き,ばねが自然長のときの物体の位置を原点とする.
時刻
での物体の位置を
として,物体の運動方程式をたてよ.ただし,加速度を
とする.
解答
閉じる
解説
ばねの自然長からの変化量を
,ばね定数を
とすると,フックの法則により,ばねにかかる弾性力は
である.(参考:水平ばね振り子)
よって,物体の運動方程式は
となる.
閉じる
解答
閉じる
解説
運動方程式を整理すると
⇒
となり,
定数係数の2階同次線形微分方程式が得られる.
上式の特性方程式
⇒
の解は
である.
特性方程式の解が虚数になるので,一般解は
となる.
この解を時刻
で微分すると,速度
を得る.ばねを
軸の正の向きに
まで伸ばして放すという初期条件より,
となり,ばねを静かに放す(初速ゼロ)という初期条件より,
⇒
となる.よって,初期条件を満たす解は
と求まる.
閉じる
解答
解説
物体が
で与えられる運動(単振動)をするとき,
は振幅にあたる.
より,物体は
で単振動する.よって振幅は
閉じる
解答
解説
もしくは,
閉じる
ばねが自然長になったときの物体の速さを求めよ.
解答
解説
で求めた解
より,速度
である.自然長(
)のとき,
なので,
である.よって,自然長になったときの物体の速さは
と求まる.
別の求め方として,力学的エネルギー保存則を用いる方法がある.振幅を
,自然長のときの物体の速さを
とすると,力学的エネルギー保存則
より,
と求まる.
閉じる
ホーム>>物理演習問題>>力学>>質点の力学>>単振動>>水平ばね振り子
学生スタッフ作成
最終更新日:2025年9月15日
 図のように,水平な滑らかな床の上で,軽いばねの一端を壁に固定して,他端に質量
の物体をつけて,ばねを水平方向に自然長から
伸ばしてから静かに放すと単振動を始めた.ここで,ばねはフックの法則に従うものとし,ばね定数を
として,
軸の正の向きを水平方向の右向き,ばねが自然長のときの物体の位置を原点とする.
図のように,水平な滑らかな床の上で,軽いばねの一端を壁に固定して,他端に質量
の物体をつけて,ばねを水平方向に自然長から
伸ばしてから静かに放すと単振動を始めた.ここで,ばねはフックの法則に従うものとし,ばね定数を
として,
軸の正の向きを水平方向の右向き,ばねが自然長のときの物体の位置を原点とする.