鉛直ばね振り子
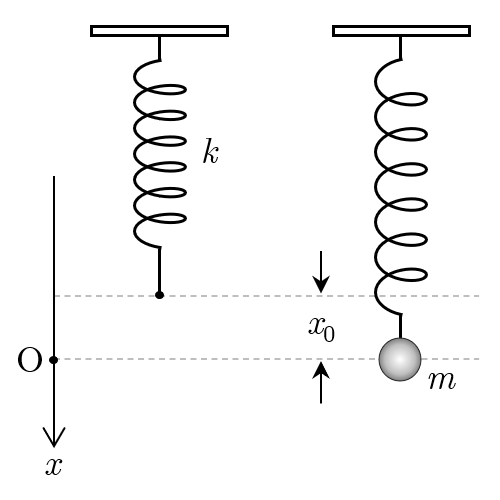 図のように,ばね定数
のばねの一端を固定して鉛直に吊るす.ばねの下端に質量
の小球をつけると,ばねの長さが
だけ伸びてつり合った.つり合いの位置を原点
とし,鉛直下向きを
軸にとる.時刻
でおもりを原点から
軸方向に長さ
だけ伸ばして静かに放すと小球は単振動した.ばねはフックの法則に従うとする.空気抵抗は無視できるものとし,重力加速度の大きさを
とする.
図のように,ばね定数
のばねの一端を固定して鉛直に吊るす.ばねの下端に質量
の小球をつけると,ばねの長さが
だけ伸びてつり合った.つり合いの位置を原点
とし,鉛直下向きを
軸にとる.時刻
でおもりを原点から
軸方向に長さ
だけ伸ばして静かに放すと小球は単振動した.ばねはフックの法則に従うとする.空気抵抗は無視できるものとし,重力加速度の大きさを
とする.
ばねの自然長から
だけ伸びてつり合う位置では,小球に働く下向きの重力と上向きの復元力がつり合う.
を
,
,
で表せ.
解答
解説
フックの法則により,自然長から
だけ伸びたときのばねの復元力は
である.これが小球に働く重力とつり合うので
が成り立つ.したがって,
と表される.
閉じる
小球の位置が
のとき,小球に作用する合力(の
成分)
を求めよ.
解答
閉じる
解説
小球の位置が
のとき,自然長からのばねの変位は
なので,このときのばねの復元力は
である.したがって,おもりに作用する合力は
(
)
となる.つまり,小球に働く力は,つり合いの位置からの変位
に比例する.
閉じる
時刻
での小球の位置を
として,小球の運動方程式をたてよ.ただし,小球の加速度(の
成分)を
とする.
解答
閉じる
解説
運動方程式
において
,
を用いると,小球の運動方程式は
となる.
閉じる
とおいて,(3)の小球の運動方程式について,初期条件を満たす解
を求めよ.(ヒント:定数係数の2階同次線形微分方程式の特性方程式をたてる.位置と速度の初期条件を用いる.)
解答
閉じる
解説
運動方程式を整理して,
とおくと
⇒
となり,定数係数の2階同次線形微分方程式が得られる.その特性方程式
の解は
である(
は虚数単位).特性方程式の解が虚数になるので,一般解は
となる.この解を時刻
で微分すると,速度
を得る.ばねを原点から
軸の正の向きに
まで伸ばして放すという初期条件より,
となり,ばねを静かに放す(初速ゼロ)という初期条件より,
⇒
となる.よって,初期条件を満たす解は
と求まる.
閉じる
小球の質量
,つり合いの位置でのばねの伸び
のとき,この単振動の周期
とばね定数
の値を求めよ.ここで,重力加速度の大きさを
とする.
解答
周期
ばね定数
閉じる
解説
周期
は
と表されるので,
,
,および
より,
を上式に代入すると,周期
を得る.また,
,
より,ばね定数
を得る.
閉じる
ホーム>>物理演習問題>>力学>>質点の力学>>単振動>>水平ばね振り子
学生スタッフ作成
最終更新日:2025年9月15日
 図のように,ばね定数
のばねの一端を固定して鉛直に吊るす.ばねの下端に質量
の小球をつけると,ばねの長さが
だけ伸びてつり合った.つり合いの位置を原点
とし,鉛直下向きを
軸にとる.時刻
でおもりを原点から
軸方向に長さ
だけ伸ばして静かに放すと小球は単振動した.ばねはフックの法則に従うとする.空気抵抗は無視できるものとし,重力加速度の大きさを
とする.
図のように,ばね定数
のばねの一端を固定して鉛直に吊るす.ばねの下端に質量
の小球をつけると,ばねの長さが
だけ伸びてつり合った.つり合いの位置を原点
とし,鉛直下向きを
軸にとる.時刻
でおもりを原点から
軸方向に長さ
だけ伸ばして静かに放すと小球は単振動した.ばねはフックの法則に従うとする.空気抵抗は無視できるものとし,重力加速度の大きさを
とする.