剛体振り子

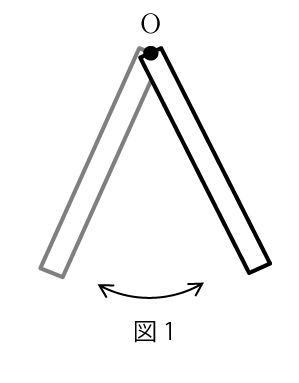
図1のように，質量

M [kg]

$M [kg]$ , 長さ

a [m]

$a [m]$ の一様な棒の一端が点

O

$O$ で固定され，鉛直面内で小さく振動している．ただし，空気抵抗は無視でき，重力加速度の大きさを

g [{m/s}^{2}]

$g [{m/s}^{2}]$ とする．

$(1)$ $(1)$ 支点 $O$ $O$ の周りの棒の慣性モーメント $I [kg \cdot m^{2}]$ $I [kg \cdot m^{2}]$ を求めよ．

解答

$I = \frac{M a^{2}}{3} [kg \cdot m^{2}]$ $I = \frac{M a^{2}}{3} [kg \cdot m^{2}]$

閉じる

解説

線密度は $\frac{M}{a}$ $\frac{M}{a}$ であり，支点 $O$ $O$ から $x$ $x$ の位置の微小質量 $d m$ $d m$ は， $d m = \frac{M}{a} d x$ $d m = \frac{M}{a} d x$ である．支点 $O$ $O$ の周りの慣性モーメント $d I$ $d I$ は， $d I = x^{2} d m = x^{2} \frac{M}{a} d x$ $d I = x^{2} d m = x^{2} \frac{M}{a} d x$
したがって慣性モーメント $I$ $I$ は，
$I = \int_{D} d I = \int_{0}^{a} x^{2} \frac{M}{a} d x = \frac{M}{a} {[\frac{x^{3}}{3}]}_{0}^{a} = \frac{M a^{2}}{3} [kg \cdot m^{2}]$ $I = \int_{D} d I = \int_{0}^{a} x^{2} \frac{M}{a} d x = \frac{M}{a} {[\frac{x^{3}}{3}]}_{0}^{a} = \frac{M a^{2}}{3} [kg \cdot m^{2}]$ となる．⇒ 詳細な説明

閉じる

$(2)$ $(2)$ 棒が鉛直面内で小さく振動するとき、単振動とみなせる．周期 $T [s]$ $T [s]$ を求めよ．

解答

$T = 2 π \sqrt{\frac{2 a}{3 g}} [s]$ $T = 2 π \sqrt{\frac{2 a}{3 g}} [s]$

閉じる

解説

この剛体棒の質量中心を $G$ $G$ とし，支点 $O$ $O$ を通る鉛直線と，直線 $OG$ $OG$ となす角を $θ$ $θ$ とする．
このとき，この剛体棒の運動方程式は， $θ \approx 0$ $θ \approx 0$ のとき， $I \frac{d^{2} θ}{d t^{2}} = - \frac{a}{2} M g \sin θ ≃ - \frac{a}{2} M g θ$ $I \frac{d^{2} θ}{d t^{2}} = - \frac{a}{2} M g \sin θ ≃ - \frac{a}{2} M g θ$ と表せる．
この棒の角振動数 $ω$ $ω$ を用いて， $\frac{d^{2} θ}{d t^{2}} = - \frac{a M g}{2 I} θ = - ω^{2} θ$ $\frac{d^{2} θ}{d t^{2}} = - \frac{a M g}{2 I} θ = - ω^{2} θ$ と表せるので， $ω = \sqrt{\frac{a M g}{2 I}}$ $ω = \sqrt{\frac{a M g}{2 I}}$
したがって， $T = \frac{2 π}{ω} = 2 π \sqrt{\frac{2 I}{a M g}} = 2 π \sqrt{\frac{2 \cdot \frac{M a^{2}}{3}}{a M g}} = 2 π \sqrt{\frac{2 a}{3 g}} [s]$ $T = \frac{2 π}{ω} = 2 π \sqrt{\frac{2 I}{a M g}} = 2 π \sqrt{\frac{2 \cdot \frac{M a^{2}}{3}}{a M g}} = 2 π \sqrt{\frac{2 a}{3 g}} [s]$

閉じる

ホーム>>物理演習問題>>力学>>剛体の力学>>剛体の平面運動>>剛体振り子

2024年10月9日