円柱の慣性モーメント

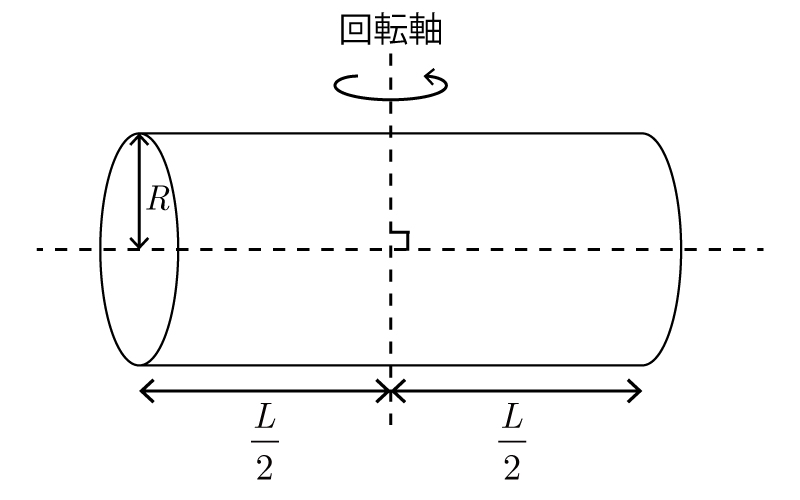
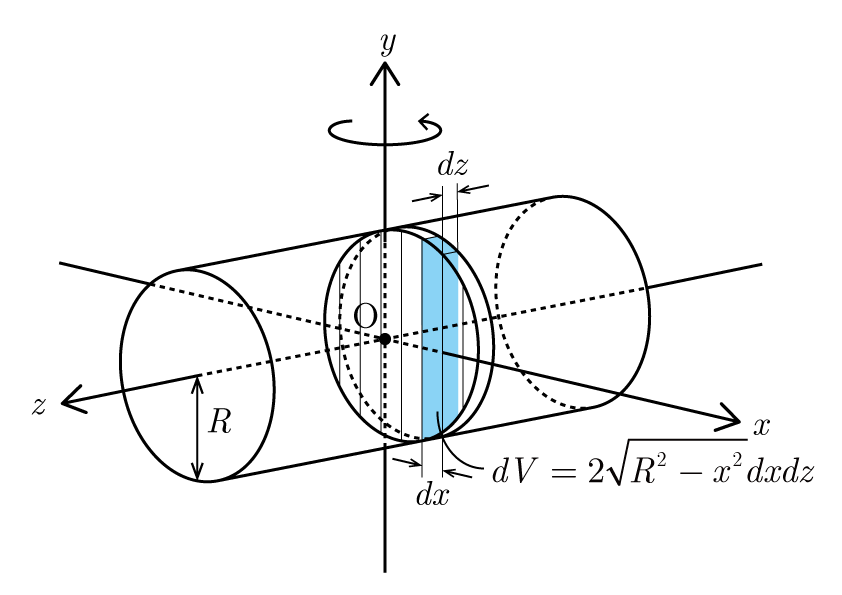
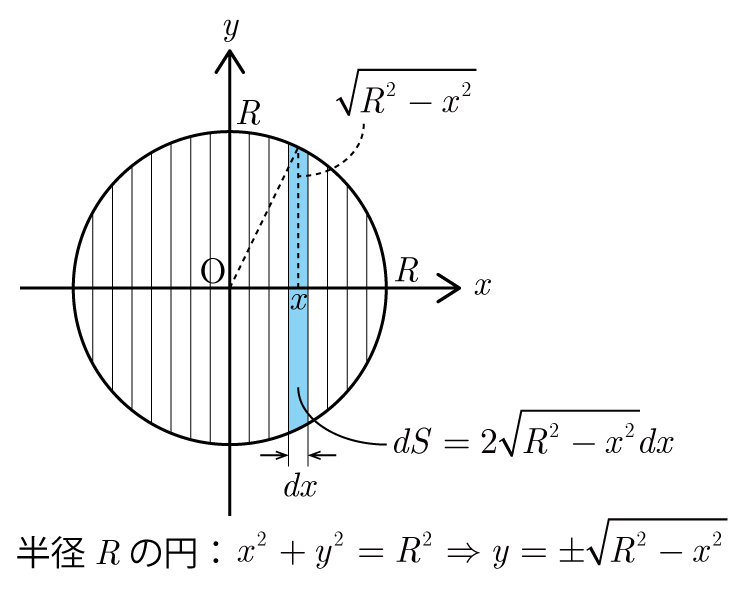
図のように回転軸を y 軸にとり， y 軸と直交する zx 平面をとる．円柱の密度を ρ とすると

ρ= MπR2L

である．この円柱を z 軸方向に微小厚み dz でスライスし，この厚み dz の円板部分をさらに x 軸方向に幅 dx で分割する．断面積 dxdz の微小角柱の長さは 2 R2 −x2 であるので，この部分の質量を dm とおくと，

dm=ρ⋅2 R2 −x2 ⋅dxdz = M πR2L ⋅2 R2 −x2 dxdz = 2M πR2L R2 −x2 dxdz

となる．

y 軸の先から円柱を見た図

y 軸の先から円柱を見た図から分かるように，この微小角柱の回転軸までの距離(回転半径)は r= x2+z2 であるので，微小角柱の回転軸周りの慣性モーメント dI は，

dI= r2dm = ( x2 +z2 ) ⋅ 2M πR2L R2 −x2 dxdz

と表せる．したがって，求める慣性モーメント I は，

I= ∫D dI = ∫D r2dm = ∫ −L2 L2 ∫−RR ( x2 +z2 )⋅ M πR2L ⋅2 R2 −x2 dx dz = 2M πR2L ∫−RR R2 −x2 { ∫ −L2 L2 ( x2 +z2 ) dz } dx

となる．ここで，

∫ −L2 L2 ( x2 +z2 )dz =2 ∫0 L2 ( x2 +z2 ) dz =2 [ x2z +13 z3 ] 0 L2 =2 { x2 ⋅L2 +13 ( L2 ) 3 } =Lx2 + L3 12

より，次式を得る．

I= 2M πR2L ∫−RR R2 −x2 ( Lx2 + L3 12 ) dx = 2M πR2 ∫−RR R2 −x2 ( x2 + L2 12 )dx

次に， x=Rsinθ とおくような置換積分を考えると， θ についての積分範囲は

となり，形式的に

dx dθ = d dθ Rsinθ=Rcosθ⇒dx=Rcosθdθ

と書けるので

∫ −R R R2 −x2 ( x2 + L2 12 )dx = ∫ −π2 π2 R2 −R2 sin2 θ ⋅ ( R2 sin2 θ+ L2 12 ) Rcosθdθ =R4 ∫ −π2 π2 cos2 θ ( 1− cos 2 θ )dθ + R2L2 12 ∫ − π2 π2 cos2 θdθ =R4 ⋅2 ∫ 0 π2 ( cos2 θ− cos4 θ )dθ + R2 L2 12 ⋅2 ∫0 π2 cos2 θdθ
↓ ここで，ウォリスの公式を利用
=2R4 ( 12 ⋅π2 −34 ⋅12 ⋅π2 ) + R2 L2 6 ⋅12 ⋅π2 = πR4 8 + πR2 L2 24

を得る．したがって，

I= 2M πR2 ( πR2 8 + πR2 L2 24 ) = MR2 4 + ML2 12

が求まる．

★ 極座標を用いて計算

円柱を z 軸方向に微小厚み dz でスライスしたときの円板について，極座標を用いて，微小部分に分割すると，その微小体積は

dV=dSdz = rdrdθdz

となるので，この部分の微小質量は

dm= ρ⋅ rdrdθdz = M πR2L ⋅ rdrdθdz

である．この微小部分の回転軸までの距離（回転半径）は

u= x2 +z2 = ( rcosθ ) 2 + z2

となるので，微小部分の，回転軸周りの慣性モーメント dI は

dI =u2 dm = ( r2 cos2 θ+ z2 ) ⋅ M πR2L ⋅rdrdθ dz

と表せる．したがって，求める慣性モーメント I は，

I= ∫ V dI = ∫ V u 2 dm = ∫ − L 2 L 2 ∫ 0 2π ∫ 0 R ( r 2 cos 2 θ+ z 2 ) M π R 2 L rdr dθ dz = M π R 2 L ∫ − L 2 L 2 { ∫ 0 2π ( ∫ 0 R ( r 3 cos 2 θ+r z 2 )dr )dθ }dz = M π R 2 L ∫ − L 2 L 2 { ∫ 0 2π [ 1 4 r 4 cos 2 θ+ 1 2 r 2 z 2 ] 0 R dθ }dz = M π R 2 L ∫ − L 2 L 2 { ∫ 0 2π ( 1 4 R 4 cos 2 θ+ 1 2 R 2 z 2 ) dθ }dz = M 2πL ∫ − L 2 L 2 { ∫ 0 2π [ 1 4 R 2 ( 1+cos2θ )+ z 2 ] dθ }dz = M 2πL ∫ − L 2 L 2 [ 1 4 R 2 ( θ+ sin2θ 2 )+θ z 2 ] 0 2π dz = M 2πL ∫ − L 2 L 2 ( π 2 R 2 +2π z 2 )dz = M L ∫ − L 2 L 2 ( 1 4 R 2 + z 2 )dz = M L [ 1 4 R 2 z+ 1 3 z 3 ] − L 2 L 2 = M L ( 1 4 R 2 L+ 1 12 L 3 ) = M R 2 4 + M L 2 12

となる．

★ 平行軸の定理を用いて計算

図に示すように，中心が原点となるように xy 平面に置かれた厚さ dz の一様な円板の， y 軸のまわりの慣性モーメント d I G は，

dIG = ∫ S ( rcosθ ) 2 ρdV = ∫ 0 2π ∫0R r2 cos2 θ M πR2 L rdrdθ dz = M πR2L ∫ 0 2π { ∫0R r3 dr } cos2 θdθ dz = M πR2L ∫02π ( 14 R4 ) cos2 θdθ dz = MR2 4πL ∫ 0 2π cos2 θdθ dz = MR2 4πL ∫ 0 2π ( 1+cos2θ 2 )dθ dz = M R 2 4πL [ θ2 + sin2θ 4 ] 0 2π dz = MR2 4L dz

である．原点 O から z 軸方向に z だけ移動した厚さ dz の円板の慣性モーメント dIz は，平行軸の定理により，

dIz =dIG + M πR2L ⋅πR2 dz⋅ |z| 2 = MR2 4L dz+ ML z2 dz

であるので，求める慣性モーメント I は，

I= ∫z dIz = ∫ − L2 L2 ( MR2 4L +ML z2 )dz = [ MR2 4L z+ M3L z3 ] −L2 L2 = MR2 4 + ML2 12

となる．