グラフと仕事 1
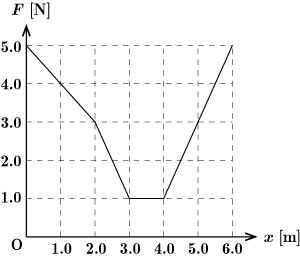 図1
図1
滑らかで水平な床の上にある小物体に,水平方向の力
を加えた.この力の向きに
軸をとり,加える力
を位置
に応じて変えると,図1に示すような
グラフが得られた.ここで,力は常に
軸に平行であるものとする.以下の問に答えよ.
位置
から
までに,この力が小物体にした仕事を求めよ.
解答
解説
 図2
図2
物体にはたらく
軸方向の力
が物体の位置
によって変化する場合,初期位置を
,最終位置を
とすると,仕事は一般に
のように
積分で表される.これは図2に示すように,
グラフが
軸との間につくる面積に対応する(斜線部分).
 図3
図3
したがって,この問題の場合,小物体が位置
から
までに移動したときの仕事は,図3の斜線部分の台形の面積で表され,
と求まる.
閉じる
位置
から
までに,この力が小物体にした仕事を求めよ.
解答
解説
 図4
図4
の解説で説明したように,小物体がした仕事は斜線部分の面積に対応する.
の解答から,位置
から
までの仕事は
であり,位置
から
までの仕事
,
位置
から
までの仕事
,
位置
から
までの仕事
となる.したがって,すべて足し合わせると
と求まる.
閉じる
位置
において,小物体は
軸の正の向きに運動しており,そのときの小物体の運動エネルギーが
であった.位置
における小物体の運動エネルギーを求めよ.
解答
解説
の解説より,外力
が位置
から
までに物体にした仕事は,
で表された.
位置
での速さを
,位置
での速さを
とすると,この仕事
と運動エネルギーの関係は
である.上式右辺の第1項目は位置
での物体の運動エネルギー,第2項目は位置
での物体の運動エネルギーである.この式より,
で求めた仕事
は,
から,
に移動したときの運動エネルギーの増分に対応することが分かる.したがって,位置
における小物体の運動エネルギーは
と求まる.
閉じる
ホーム>>物理演習問題>>力学>>仕事・エネルギー>>仕事>>F-xグラフと仕事 1
学生スタッフ作成
最終更新日:2025年7月31日



