等加速度直線運動の式の導出(応用)
時刻
t
〔s〕
を横軸,速度
v
〔m/s〕
を縦軸としてグラフで表したのが
v-t
グラフである.
等加速度直線運動の場合,線の傾きが加速度
a
〔m/
s2〕
であり,ある時刻
t
a
〔 s 〕
からある時刻
t
b
〔 s 〕
とグラフ線と
t=0
で囲んだ面積が移動距離
Δx
〔
m
〕
となる.
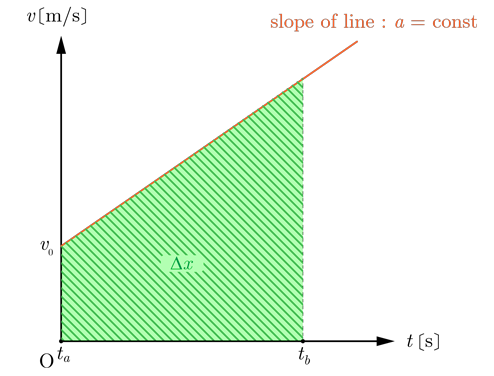
等加速度直線運動の式の導出では,初速度の大きさ
v
0
〔m/s〕
,時刻
t
〔s〕 が
0
から
t
まで等加速度直線運動したのときの移動距離
Δ x
〔
m
〕
を求めたが,このページでは初速度の大きさ
v
0
=0
〔m/s〕
,時刻
t
〔s〕 が
0
から
t
まで等加速度直線運動したのときの移動距離
Δx
〔
m
〕
と,初速度の大きさ
v
0
〔m/s〕
,時刻
t
〔s〕
が
t
a
から
t
b
まで等加速度直線運動したのときの移動距離
Δ x
〔
m
〕
の求め方を解説する.
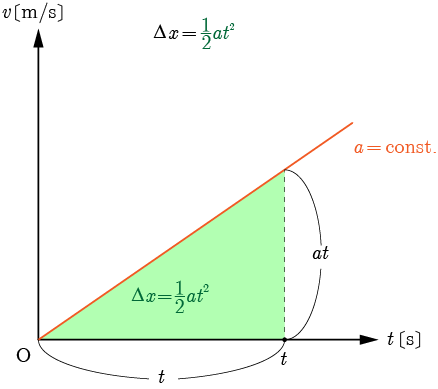
初速度の大きさ
v
0
=0
〔m/s〕
,時刻
t
〔s〕 が
0
から
t
まで等加速度直線運動したのときの移動距離
Δ x
〔
m
〕
は,底辺を
t
,高さを
at
とした三角形の面積を求める方法で導き出せる.
よって移動距離
Δ x
〔
m
〕
は
Δ x=
1
2
a
t
2
さらに
x=
x
0
+Δx
より
x=
x
0
+
1
2
a
t
2
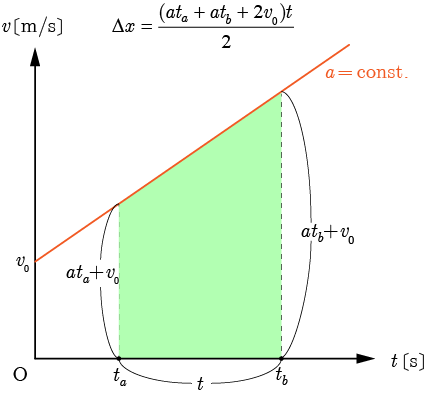
初速度の大きさ
v
0
〔m/s〕
,時刻
t
〔s〕
が
t
a
から
t
b
まで等加速度直線運動したのときの移動距離
Δ x
〔
m
〕
は,上底を
a
t
a
+
v
0
下底を
a
t
b
+
v
0
高さを
t
とした台形の面積を求める方法で導き出せる.
よって移動距離
Δ x
〔
m
〕
は
Δx=
(a
t
a
+a
t
b
+2
v
0
)t
2
=
v
0
t+
t
a
+
t
b
2
at
さらに
x=
x
0
+Δx
より
x=
x
0
+
v
0
t+
t
a
+
t
b
2
at
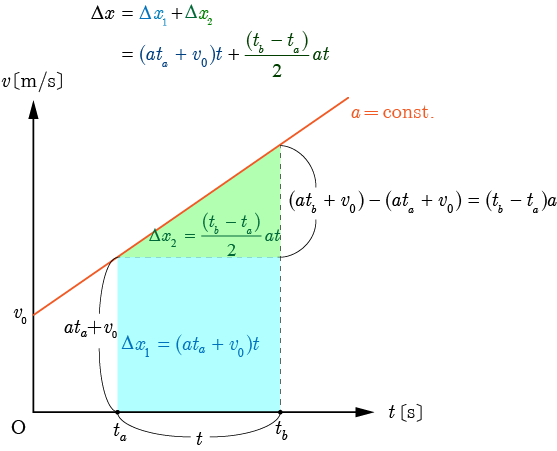
また別解として底辺を
t
高さを
(
t
b
−
t
a
)a
とした三角形の面積と縦を
a
t
a
+
v
0
横を
t
とした長方形の面積を足す方法がある.
この場合の
移動距離
Δ x
〔
m
〕
も
Δx=(a
t
a
+
v
0
)t+
t
b
−
t
a
2
at
=
v
0
t+
2
2
a
t
a
⋅t+
t
b
−
t
a
2
at
=
v
0
t+
2
t
a
+(
t
b
−
t
a
)
2
at
=
v
0
t+
t
a
+
t
b
2
at
さらに
x=
x
0
+Δx
より
x=
x
0
+
v
0
t+
t
a
+
t
b
2
at
ホーム>>物理基礎>>第1編 物体の運動とエネルギー>>第1章 物体の運動>>v-tグラフからxを求める方法
学生スタッフ作成
2016年3月28日
|




