平面上の速度

速度のページでは，直線上を運動する物体の速度の説明をした．このページでは，平面上の速度(Velocity on a plane)について説明する．

平面上を運動する物体の速度は，大きさと向きの両方をもつためベクトル量(Vector quantity)である．よって，速度ベクトル ${\displaystyle \overrightarrow{v}}$ は， ${\displaystyle x}$ 方向，${\displaystyle y}$ 方向のそれぞれの成分を用いて，

${\displaystyle \overrightarrow{v}=\left(v_x,v_y\right)}$

${\displaystyle \left|\overrightarrow{v}\right|=\sqrt{v_x^2+v_y^2}}$

平面上を運動する物体の，時刻 ${\displaystyle t_1〔\text{s}〕}$ での位置を ${\displaystyle x_1〔\text{m}〕}$ ， ${\displaystyle y_1〔\text{m}〕}$ ，時刻 ${\displaystyle t_2〔\text{s}〕}$ での位置を ${\displaystyle x_2〔\text{m}〕}$ , ${\displaystyle y_2〔\text{m}〕}$ とする． ${\displaystyle \Delta x=x_2-x_1}$ ， ${\displaystyle \Delta y=y_2-y_1}$ ， ${\displaystyle \Delta t=t_2-t_1}$ とおくと， 平均の速度(Average velocity)は

${\displaystyle \overrightarrow{\overline{v}}=({\overline{v}}_x,{\overline{v}}_y)}$ ${\displaystyle =(\frac{x_2-x_1}{t_2-t_1},\frac{y_2-y_1}{t_2-t_1})}$ ${\displaystyle =(\frac{\Delta x}{\Delta t},\frac{\Delta y}{\Delta t})}$

で表される．

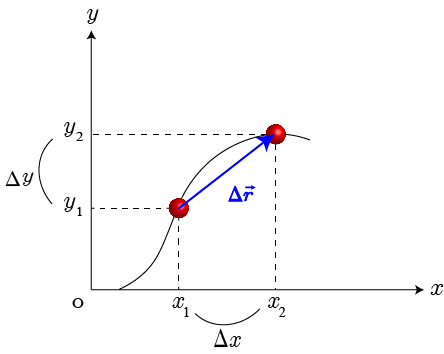
上の平均の速度の式において， ${\displaystyle t_2}$ を ${\displaystyle t_1}$ に限りなく近づける，つまり ${\displaystyle \Delta t=t_2-t_1}$ を限りなくゼロに近づけると， ${\displaystyle \overrightarrow{\overline{v}}〔\text{m}/{\text{s}}^2〕}$ は時刻 ${\displaystyle t_1〔\text{s}〕}$ における速度(瞬間の速度)(Velocity of the moment)は

${\displaystyle \overrightarrow{v}(t_1)}$ ${\displaystyle =\underset{t_2\to t_1}{\lim }\frac{{\overrightarrow{r}}_2-{\overrightarrow{r}}_1}{t_2-t_1}}$ ${\displaystyle =\underset{\Delta t\to 0}{\lim }\frac{\Delta \overrightarrow{r}}{\Delta t}}$

となる．したがって，任意の時刻${\displaystyle t〔\text{s}〕}$ における速度(瞬間の速度)は，

${\displaystyle \overrightarrow{v}(t)}$ ${\displaystyle =\underset{\Delta t\to 0}{\lim }\frac{\overrightarrow{r}(t+\Delta t)-\overrightarrow{r}(t)}{\Delta t}}$ ${\displaystyle =\frac{d\overrightarrow{r}}{dt}=\left(\frac{dx}{dt},\frac{dy}{dt}\right)}$

で与えられる．

ホーム>>物理>>第1編　力と運動>>第2章　平面上の運動と放物運動>>平面上の速度

学生スタッフ作成

2018年3月1日