2次元における $n$ 質点系の重心の導出(別解)

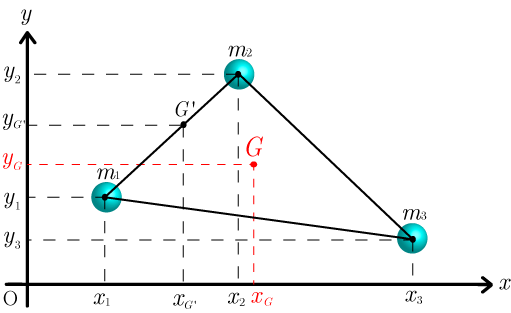
2次元における3質点系の重心において，重心の座標を重心Gのまわりの3質点系のつり合い条件より導いた．

ここでは，異なる手法として，2質点系の重心の座標を繰り返し導出することで，3質点系の重心の座標を導く．

3質点の質量を $m_{1} 〔 k g 〕$ ， $m_{2} 〔 k g 〕$ ， $m_{3} 〔 k g 〕$ とし，座標をそれぞれ $(x_{1}, y_{1}) 〔 m 〕$ ， $(x_{2}, y_{2}) 〔 m 〕$ ， $(x_{3}, y_{3}) 〔 m 〕$ と置く．質点 $m_{1} 〔 k g 〕$ と質点 $m_{2} 〔 k g 〕$ の重心G'の座標を $(x_{G'}, y_{G'}) 〔 m 〕$ とすると，2質点系の重心(2次元)より，

$(x_{G'}, y_{G'})$ $= (\frac{m_{1} x_{1} + m_{2} x_{2}}{m_{1} + m_{2}}, \frac{m_{1} y_{1} + m_{2} y_{2}}{m_{1} + m_{2}}) 〔 m 〕$

2質点 $m_{1} + m_{2} 〔 kg 〕$ の重心 $(x_{G'}, y_{G'})$ と，質点 $m_{３} 〔 k g 〕$ の座標 $(x_{3}, y_{3}) 〔 m 〕$ に対する重心Gの座標 $(x_{G}, y_{G}) 〔 m 〕$ は，2質点系の重心(2次元)より，

$x_{G} = \frac{(m_{1} + m_{2}) x_{G'} + m_{3} x_{3}}{(m_{1} + m_{2}) + m_{3}}$ $= \frac{(m_{1} + m_{2}) \frac{m_{1} x_{1} + m_{2} x_{2}}{m_{1} + m_{2}} + m_{3} x_{3}}{m_{1} + m_{2} + m_{3}}$ $= \frac{m_{1} x_{1} + m_{2} x_{2} + m_{3} x_{3}}{m_{1} + m_{2} + m_{3}} 〔 m 〕$

$y_{G} = \frac{(m_{1} + m_{2}) y_{G'} + m_{3} y_{3}}{(m_{1} + m_{2}) + m_{3}}$ $= \frac{(m_{1} + m_{2}) \frac{m_{1} y_{1} + m_{2} y_{2}}{m_{1} + m_{2}} + m_{3} y_{3}}{m_{1} + m_{2} + m_{3}}$ $= \frac{m_{1} y_{1} + m_{2} y_{2} + m_{3} y_{3}}{m_{1} + m_{2} + m_{3}} 〔 m 〕$

これは3質点系の重心(2次元)に等しい．

一般に， $n$ 質点系の重心の座標も2質点系の重心の座標を $n - 1$ 回繰り返し導くことで得られる．

ホーム>>物理>>第1編　力と運動>>第1章　剛体>>2次元における $n$ 質点系の重心の導出(別解)

学生スタッフ作成

2025年10月21日

2次元における n 質点系の重心の導出(別解)

2次元における $n$ 質点系の重心の導出(別解)