立方体の影の作図問題　解答(4)

■問題(4)

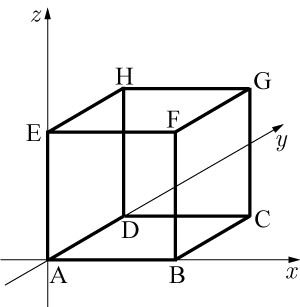
図のような一辺の長さが $1$ mの立方体がある．頂点 $A$ を原点に，対角線 $A G$ が $z$ 軸と重なり，平面 $A C G E$ が $y z$ 平面と一致し，頂点 $C$ の座標の $y$ 成分が正になるように，すなわち北側になるように，頂点 $E$ の座標の $y$ 成分が負になるように，すなわち南側になるように立方体を地表面に設置した(下図を参照せよ)．立方体の影をグラフ用紙に作図せよ．グラフ用紙には東西南北の方角を明記する．また， $1$ mの長さが $5$ cmになるように作図する．作図に必要な計算を記入しておくこと．

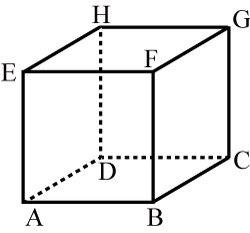立方体

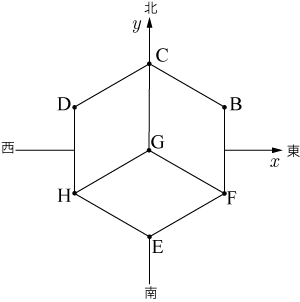立方体を真上から見た状態
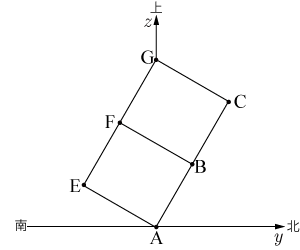立方体を東から見た状態

■答

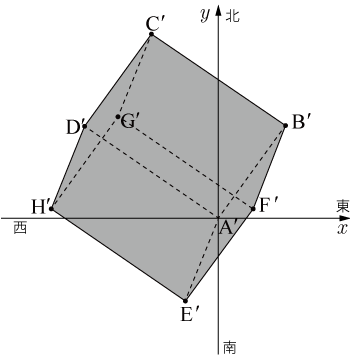
■解き方

地面に配置した立方体は下図のように $x y$ 平面上に置いた立方体を $z$ 軸の周りに $45 °$ 回転させた後， $x$ 軸の周りに $∠ E A C$ 回転させたものである．

$z$ 軸に $∠ E A C$ 回転させる1次変換の表現行列を $R_{z}$ とすると

$R_{z} = (\begin{matrix} cos 45 ° & - sin 45 ° & 0 \\ sin 45 ° & cos 45 ° & 0 \\ 0 & 0 & 1 \end{matrix}) = (\begin{matrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 1 \end{matrix})$

となる．

$∠ E A G = θ$ とする． $x$ 軸の周りに $θ$ 回転させる1次変換の表現行列を $R_{x}$ とすると

$R_{x} = (\begin{matrix} 1 & 0 & 0 \\ 0 & cos θ & - sin θ \\ 0 & sin θ & cos θ \end{matrix})$

$sin θ = \sqrt{\frac{2}{3}}$ ， $cos θ = \frac{1}{\sqrt{3}}$

よって

$R_{x} = (\begin{matrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & - \sqrt{\frac{2}{3}} \\ 0 & \sqrt{\frac{2}{3}} & \frac{1}{\sqrt{3}} \end{matrix})$

となる．

したがって $z$ 軸の周りに $45 °$ 回転させた後， $x$ 軸の周りに $θ$ 回転させる1次変換の表現行列は $R_{x} R_{z}$ となる．

$R_{x} R_{z} = (\begin{matrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & - \sqrt{\frac{2}{3}} \\ 0 & \sqrt{\frac{2}{3}} & \frac{1}{\sqrt{3}} \end{matrix}) (\begin{matrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 1 \end{matrix}) = (\begin{matrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & - \sqrt{\frac{2}{3}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{matrix})$

1次変換する前の各頂点の座標は

$A (0, 0, 0,)$ $E (0, 0, 1)$

$B (1, 0, 0)$ $F (1, 0, 1)$

$C (1, 1, 0)$ $G (1, 1, 1)$

$D (0, 1, 0)$ $H (0, 1, 1)$

である．よって1次変換後(問題文の図4，図5の状態)の各頂点の座標は

$(\begin{matrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & - \sqrt{\frac{2}{3}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{matrix}) (\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}) = (\begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{6}} \\ \frac{1}{\sqrt{3}} \end{matrix})$ $B (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{6}}, \frac{1}{\sqrt{3}})$

$(\begin{matrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & - \sqrt{\frac{2}{3}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{matrix}) (\begin{matrix} 1 \\ 1 \\ 0 \end{matrix}) = (\begin{matrix} 0 \\ \frac{2}{\sqrt{6}} \\ \frac{2}{\sqrt{3}} \end{matrix}) = (\begin{matrix} 0 \\ \sqrt{\frac{2}{3}} \\ \frac{2}{\sqrt{3}} \end{matrix})$ $C (0, \sqrt{\frac{2}{3}}, \frac{2}{\sqrt{3}})$

$(\begin{matrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & - \sqrt{\frac{2}{3}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{matrix}) (\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}) = (\begin{matrix} - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{6}} \\ \frac{1}{\sqrt{3}} \end{matrix})$ $D (- \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{6}}, \frac{1}{\sqrt{3}})$

$(\begin{matrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & - \sqrt{\frac{2}{3}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{matrix}) (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}) = (\begin{matrix} 0 \\ - \sqrt{\frac{2}{3}} \\ \frac{1}{\sqrt{3}} \end{matrix})$ $E (0, - \sqrt{\frac{2}{3}}, \frac{1}{\sqrt{3}})$

$(\begin{matrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & - \sqrt{\frac{2}{3}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{matrix}) (\begin{matrix} 1 \\ 0 \\ 1 \end{matrix}) = (\begin{matrix} \frac{1}{\sqrt{2}} \\ - \frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{3}} \end{matrix})$ $F (\frac{1}{\sqrt{2}}, - \frac{1}{\sqrt{6}}, \frac{2}{\sqrt{3}})$

$(\begin{matrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & - \sqrt{\frac{2}{3}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{matrix}) (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ \sqrt{3} \end{matrix})$ $G (0, 0, \sqrt{3})$

$(\begin{matrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & - \sqrt{\frac{2}{3}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{matrix}) (\begin{matrix} 0 \\ 1 \\ 1 \end{matrix}) = (\begin{matrix} - \frac{1}{\sqrt{2}} \\ - \frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{3}} \end{matrix})$ $H (- \frac{1}{\sqrt{2}}, - \frac{1}{\sqrt{6}}, \frac{2}{\sqrt{3}})$

となる．

次に各頂点の影の位置を(3)で求めた表現行列を使って計算する．点 $A$ の影を点 $A^{'}$ と表すことにする．

$(\begin{matrix} 1 & 0 & - \frac{1}{\sqrt{6}} \\ 0 & 1 & \frac{1}{\sqrt{6}} \\ 0 & 0 & 0 \end{matrix}) (\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ 0 \end{matrix})$ $A^{'} (0, 0, 0)$

$(\begin{matrix} 1 & 0 & - \frac{1}{\sqrt{6}} \\ 0 & 1 & \frac{1}{\sqrt{6}} \\ 0 & 0 & 0 \end{matrix}) (\begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{6}} \\ \frac{1}{\sqrt{3}} \end{matrix}) = (\begin{matrix} \frac{1}{\sqrt{2}} - \frac{1}{3 \sqrt{2}} \\ \frac{1}{\sqrt{6}} + \frac{1}{3 \sqrt{2}} \\ 0 \end{matrix}) = (\begin{matrix} \frac{\sqrt{2}}{3} \\ \frac{\sqrt{3} + 2}{3 \sqrt{2}} \\ 0 \end{matrix})$ $B^{'} (\frac{\sqrt{2}}{3}, \frac{\sqrt{6} + \sqrt{2}}{6}, 0)$

$(\begin{matrix} 1 & 0 & - \frac{1}{\sqrt{6}} \\ 0 & 1 & \frac{1}{\sqrt{6}} \\ 0 & 0 & 0 \end{matrix}) (\begin{matrix} 0 \\ \sqrt{\frac{2}{3}} \\ \frac{2}{\sqrt{3}} \end{matrix}) = (\begin{matrix} - \frac{\sqrt{2}}{3} \\ \frac{\sqrt{6} + \sqrt{2}}{3} \\ 0 \end{matrix})$ $C^{'} (- \frac{\sqrt{2}}{3}, \frac{\sqrt{6} + \sqrt{2}}{3}, 0)$

$(\begin{matrix} 1 & 0 & - \frac{1}{\sqrt{6}} \\ 0 & 1 & \frac{1}{\sqrt{6}} \\ 0 & 0 & 0 \end{matrix}) (\begin{matrix} - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{6}} \\ \frac{1}{\sqrt{3}} \end{matrix}) = (\begin{matrix} - \frac{2 \sqrt{2}}{3} \\ \frac{\sqrt{3} + 1}{3 \sqrt{2}} \\ 0 \end{matrix})$ $D^{'} (- \frac{2 \sqrt{2}}{3}, \frac{\sqrt{6} + \sqrt{2}}{6}, 0)$

$(\begin{matrix} 1 & 0 & - \frac{1}{\sqrt{6}} \\ 0 & 1 & \frac{1}{\sqrt{6}} \\ 0 & 0 & 0 \end{matrix}) (\begin{matrix} 0 \\ - \sqrt{\frac{2}{3}} \\ \frac{1}{\sqrt{3}} \end{matrix}) = (\begin{matrix} - \frac{1}{3 \sqrt{2}} \\ \frac{- 2 \sqrt{3} + 1}{3 \sqrt{2}} \\ 0 \end{matrix})$ $E^{'} (- \frac{\sqrt{2}}{6}, \frac{- 2 \sqrt{6} + \sqrt{2}}{6}, 0)$

$(\begin{matrix} 1 & 0 & - \frac{1}{\sqrt{6}} \\ 0 & 1 & \frac{1}{\sqrt{6}} \\ 0 & 0 & 0 \end{matrix}) (\begin{matrix} \frac{1}{\sqrt{2}} \\ - \frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{3}} \end{matrix}) = (\begin{matrix} \frac{1}{3 \sqrt{2}} \\ \frac{- \sqrt{3} + 2}{3 \sqrt{2}} \\ 0 \end{matrix})$ $F^{'} (\frac{\sqrt{2}}{6}, \frac{- \sqrt{6} + 2 \sqrt{2}}{6}, 0)$

$(\begin{matrix} 1 & 0 & - \frac{1}{\sqrt{6}} \\ 0 & 1 & \frac{1}{\sqrt{6}} \\ 0 & 0 & 0 \end{matrix}) (\begin{matrix} 0 \\ 0 \\ \sqrt{3} \end{matrix}) = (\begin{matrix} - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ 0 \end{matrix})$ $G^{'} (- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}, 0)$

$(\begin{matrix} 1 & 0 & - \frac{1}{\sqrt{6}} \\ 0 & 1 & \frac{1}{\sqrt{6}} \\ 0 & 0 & 0 \end{matrix}) (\begin{matrix} - \frac{1}{\sqrt{2}} \\ - \frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{3}} \end{matrix}) = (\begin{matrix} - \frac{5}{3 \sqrt{2}} \\ \frac{- \sqrt{3} + 2}{3 \sqrt{2}} \\ 0 \end{matrix})$ $H^{'} (- \frac{5 \sqrt{2}}{6}, \frac{- \sqrt{6} + 2 \sqrt{2}}{6}, 0)$

以上求めたデータを用いて影を描くと下図のようになる．

ホーム>>カテゴリー分類>>行列>>線形代数>>線形代数に関する問題>>線形写像・1次変換>>立方体の影の作図問題>>(4)の解答

作成：学生スタッフ
最終更新日： 2025年4月25日

立方体の影の作図問題 解答(4)

■問題(4)

■答

■解き方

立方体の影の作図問題　解答(4)