2次関数のグラフの式を求める問題

■問題

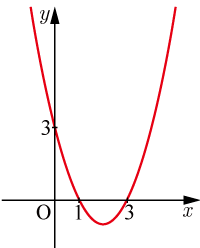
図は $x$ 切片が $1$ ， $3$ , $y$ 切片が $3$ の2次関数のグラフである．グラフを表す2次関数の式を求めよ．

■答

${\displaystyle y=\left(x-1\right)\left(x-3\right)}$

■ヒント

グラフの $x$ 切片が $\alpha$ ， $\beta$ である2次関数を参照

■解説

$x$ 切片が $1$ ， $3$より，2次関数は一般的に

${\displaystyle y=a\left(x-1\right)\left(x-3\right)}$　･･････(1)

ただし， $a$ は定数

と表される．

$y$ 切片が $3$ より，(1)に $x=0$ ， $y=3$ を代入する．

${\displaystyle 3=a\left(0-1\right)\left(0-3\right)}$

${\displaystyle 3=3a}$

${\displaystyle a=1}$　･･････(2)

(1)に(2)を代入する．

${\displaystyle y=\left(x-1\right)\left(x-3\right)}$　･･････(3)

(3)が求める2次関数の式になる．

■別解

2次関数は一般的に

${\displaystyle y=a{x}^2+bx+c}$　･･････(4)

と表される．

$x$ 切片が $1$ ， $3$ , $y$ 切片が $3$ より

• $x=1$ のとき $y=0$
• $x=3$ のとき $y=0$
• $x=0$ のとき $y=3$

となるので，以下の連立方程式が成り立つ．

この連立方程式を解く

（5)，(6)に(7)を代入する．

${\displaystyle a+b+3=0}$　･･････(8)

${\displaystyle {\displaystyle 9a+3b+3=0}}$　･･････(9)

(8)より

${\displaystyle b=-a-3}$　･･････(10)

(10)を(9)に代入する．

${\displaystyle 9a+3\left(-a-3\right)+3=0}$

${\displaystyle 6a-6=0}$

${\displaystyle a=1}$　･･････(11)

(11)を(10)に代入する．

${\displaystyle 1+b+3=0}$

${\displaystyle b=-4}$　･･････(12)

(7)，(11)，(12)を(4)に代入する．

${\displaystyle y=x^2-4x+3}$　･･････(13)

(13)が求める2次関数である．(13)を因数分解すると(3)になる．

 

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>1次関数，2次関数などに関する問題>>2次関数のグラフの式を求める問題

最終更新日： 2024年9月13日