2次不等式に関する問題

■問題

2次不等式

${\displaystyle -x^2+x+72>0}$ 　･･････(1)

の解を求めよ．

■答

$-8<x<9$

■解説

(1)の2次不等式の $x^2$ の係数が負である． 2次不等式を解く場合， $x^2$ の係数が正になるように式を変形すると， $x^2$ の係数が正場合と同様に解くことができる．よって，(1)の不等式の両辺に $-1$ を掛ける．このとき不等号の向きが変わることに注意する（不等号の性質5）．

$x^2-x-72<0$　･･････(2)

(2)の左辺を因数分解すると

$\left(x+8\right)\left(x-9\right)<0$ 　･･････(3)

となる． $x^2-x-72$ の因数分解についてはこのページを参照する．詳しく解説をしている．

(3)の不等式が成り立つのは

$x+8>0$ ，かつ， $x-9<0$ の場合　･･････(I)

あるいは

$x+8<0$ ，かつ， $x-9>0$ の場合　･･････(II)

である．

（I)より

$x>-8$ ，かつ， $x<9$

図で示すと

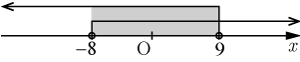
すなわち

$-8<x<9$ 　･･････(3)

となる．

（II)より

$x<-8$ ，かつ， $x>9$

図で示すと

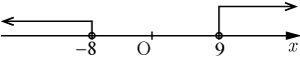
すなわち

解なし　･･････(4)

となる．

以上，(3)と(4)より，(1)の不等式の解は

$-8<x<9$

となる．

●グラフを用いた確認

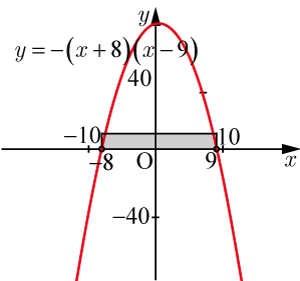
$y=-x^2+x+72$ $=-\left(x+8\right)\left(x-9\right)$　･･････(5)

とおき，(1)の解と(5)グラフの関係を確認すと，(1)を満たす部分は，グラフの $x$ 軸より上の部分になり，容易に解の範囲を理解するができる．

 

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>方程式・不等式に関する問題>>2次不等式に関する問題

最終更新日： 2024年10月1日