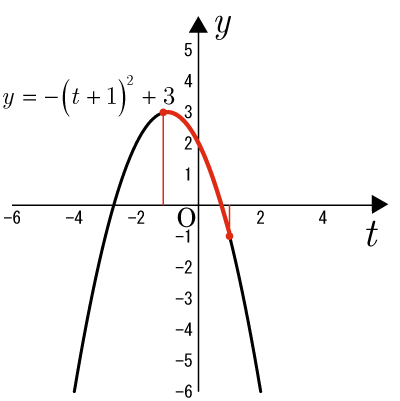三角関数の最大値・最小値に関する問題

■問題

次の関数の最大値と最小値を求めよ．ただし， ${\displaystyle 0\leqq \theta \leqq 2\pi }$ とする．

${\displaystyle y={sin}^2\theta -2cos\theta +1}$

■解説動画

◇三角関数の動画一覧のページへ

■答

${\displaystyle \theta =\pi }$ のとき，最大値  ${\displaystyle 3}$

$\theta =0,2\pi$ のとき，最小値  ${\displaystyle -1}$

■ヒント

公式 ${\displaystyle {sin}^2\theta +{cos}^2\theta =1}$ を利用して， ${\displaystyle cos\theta }$ に統一する．

${\displaystyle cos\theta }$ を ${\displaystyle t}$ と置き換えて計算を行う．

2次関数の最大と最小(範囲指定あり）を参照する．

増減表を用いて解くこともできる．

■解説

${\displaystyle {sin}^2\theta +{cos}^2\theta =1}$ より

${\displaystyle {\sin }^2\theta =1-{\cos }^2\theta }$ ･･････(1)

与式に(1)を代入すると

${\displaystyle y=\left(1-{cos}^2\theta \right)-2cos\theta +1}$

${\displaystyle y=-{cos}^2\theta -2cos\theta +2}$ ･･････(2)

となる． ${\displaystyle \cos \theta =t}$ とおいて，(2)に代入する．

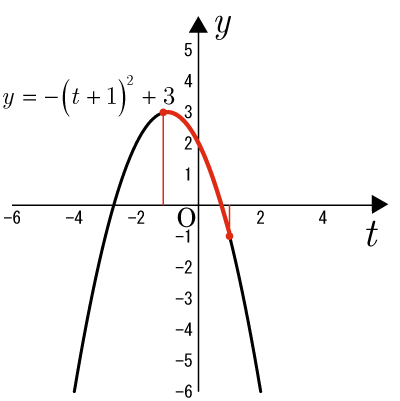
${\displaystyle y=-t^2-2t+2}$ ･･････(3)

(3)の2次関数を平方完成する．

${\displaystyle y=-(t^2+2t)+2}$

${\displaystyle y=-{\left(t+1\right)}^2+3}$

${\displaystyle t}$ の範囲を求める．

${\displaystyle 0\leqq \theta \leqq 2\pi }$

${\displaystyle -1\leqq \cos \theta \leqq 1}$

${\displaystyle -1\leqq t\leqq 1}$ ･･････(4)

図より， ${\displaystyle y=-{\left(t+1\right)}^2+3}$ は

${\displaystyle t=-1}$ のとき最大値  ${\displaystyle 3}$

${\displaystyle t=1}$ のとき最小値  ${\displaystyle -1}$

をとる．

$t$ に対応する ${\displaystyle \theta }$ を求める．

${\displaystyle cos\theta =-1}$  ⇒  ${\displaystyle \theta =\pi }$

${\displaystyle cos\theta =1}$  ⇒  $\theta =0,2\pi$

以上より， ${\displaystyle y={sin}^2\theta -2cos\theta +1}$ は

${\displaystyle \theta =\pi }$ のとき，最大値  ${\displaystyle 3}$

$\theta =0,2\pi$ のとき，最小値  ${\displaystyle -1}$

となる．

●増減表を用いる方法

${\displaystyle y^{\prime }=2\sin \theta \cos \theta +2\sin \theta }$${\displaystyle =2\sin \theta \left(\cos \theta +1\right)}$

$y^{\prime }=0$となるのは

${\displaystyle \sin \theta =0}$，あるいは，$\cos \theta +1=0$⇒$\cos \theta =-1$

よって

$\theta =0,\pi ,2\pi$

$0<\theta <\pi$のとき 　

$\sin \theta >0$，$\cos \theta +1>0$

$\pi <\theta <2\pi$のとき

$\sin \theta <0$，$\cos \theta +1>0$

となる．したがって，増減表は　

となる.　

以上より， ${\displaystyle y={sin}^2\theta -2cos\theta +1}$ は

${\displaystyle \theta =\pi }$ のとき，最大値  ${\displaystyle 3}$

$\theta =0,2\pi$ のとき，最小値  ${\displaystyle -1}$

となる．

${\displaystyle y={sin}^2\theta -2cos\theta +1}$ｓ のグラフを以下に示す．

　

ホーム>>カテゴリー分類>>三角関数>>三角関数の問題>>三角関数の方程式に関する問題>>三角関数の最大値・最小値に関する問題

学生スタッフ作成
最終更新日： 2025年4月18日