回転体の重心を求める問題

■問題

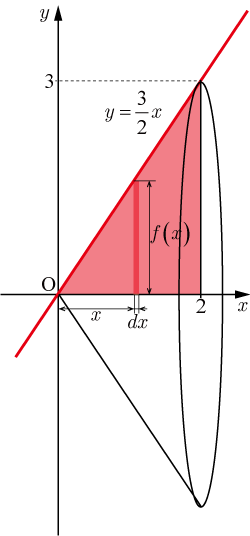
直線${\displaystyle y=\frac{3}{2}x}$ と直線$x=2$と ${\displaystyle x}$ 軸で囲まれた図形を${\displaystyle }$軸の周りに${\displaystyle 1}$ 回転してできる回転体の重心 ${\displaystyle \text{G}}$の位置を求めよ．ただし，重心 の ${\displaystyle x}$ 座標を ${\displaystyle x_{\text{G}}}$ ， ${\displaystyle y}$ 座標を ${\displaystyle y_{\text{G}}}$ とする．

■答

図形の重心 G の位置は，${\displaystyle \begin{array}{ccc}\left(x_{\text{G}},y_{\text{G}}\right)& =& \left(\frac{3}{2},0\right)\end{array}}$ 

■ヒント

回転体は円錐になる．

回転体の重心の計算より

${\displaystyle x_{\text{G}}=\frac{1}{V}{\displaystyle {\int }_a^b\pi x{\left\{f\left(x\right)\right\}}^2}dx}$

の公式を用いる．

回転体の回転軸を${\displaystyle x}$ 軸としたとき，対称性から重心 ${\displaystyle \text{G}}$は${\displaystyle x}$軸上（${\displaystyle y_{\text{G}}=0}$ ）にあるため，${\displaystyle x_{\text{G}}}$だけを求めればよい．

■解説

●回転体の体積を求める．

${\displaystyle V={\displaystyle {\int }_0^2\pi {\left\{f\left(x\right)\right\}}^{2}dx}}$

（回転体の体積の求め方は，体積の計算の${\displaystyle 2}$つ目の式を参照）

${\displaystyle ={\displaystyle {\int }_0^2\pi {\left(\frac{3}{2}x\right)}^{2}dx}}$

（${\displaystyle f\left(x\right)=\frac{3}{2}x}$を式に代入すた．）

${\displaystyle ={\displaystyle {\int }_0^2\pi ·\frac{9}{4}{x}^{2}dx}}$

${\displaystyle =\frac{9}{4}\pi {\displaystyle {\int }_0^2{x}^{2}dx}}$

${\displaystyle =\frac{9}{4}\pi {\left[\frac{1}{3}{x}^3\right]}_0^2}$

${\displaystyle =\frac{9}{4}\pi \left\{\frac{1}{3}\left(2^3-0^3\right)\right\}}$

${\displaystyle =\frac{9}{4}\pi \left(\frac{1}{3}·8\right)}$

${\displaystyle =\frac{9}{4}\pi ·\frac{8}{3}}$

${\displaystyle =6\pi }$

●${\displaystyle x_{\text{G}}}$を求める

${\displaystyle x_{\text{G}}=\frac{1}{V}{\displaystyle {\int }_0^2\pi x{\left\{f\left(x\right)\right\}}^{2}dx}}$

（ヒントの公式を参照）

${\displaystyle =\frac{1}{6\pi }{\displaystyle {\int }_0^2\pi x{\left(\frac{3}{2}x\right)}^{2}dx}}$

（${\displaystyle V=6\pi }$ と ${\displaystyle f\left(x\right)=\frac{3}{2}x}$ を式に代入した．）

${\displaystyle =\frac{1}{6\pi }{\displaystyle {\int }_0^2\pi x·\frac{9}{4}{x}^{2}dx}}$

${\displaystyle =\frac{1}{6\pi }·\frac{9}{4}\pi {\displaystyle {\int }_0^2{x}^{3}dx}}$

${\displaystyle =\frac{3}{8}{\left[\frac{1}{4}{x}^4\right]}_0^2}$

${\displaystyle =\frac{3}{8}\left\{\frac{1}{4}\left(2^4-0^4\right)\right\}}$

${\displaystyle =\frac{3}{8}\left(\frac{1}{4}·16\right)}$

${\displaystyle =\frac{3}{8}·4}$

${\displaystyle =\frac{3}{2}}$

ここで， ${\displaystyle y_{\text{G}}}$ は，重心${\displaystyle \text{G}}$が${\displaystyle x}$軸上にあるため

${\displaystyle \begin{array}{ccc}{y}_{\text{G}}& =& 0\end{array}}$

である．

よって，図形の重心${\displaystyle \text{G}}$の位置は， ${\displaystyle \begin{array}{ccc}\left(x_{\text{G}},y_{\text{G}}\right)& =& \left(\frac{3}{2},0\right)\end{array}}$ となる．

　

ホーム>>カテゴリー分類>>積分>>積分の問題>>定積分の問題>>回転体の重心を求める問題

学生スタッフ作成
最終更新日： 2023年11月24日