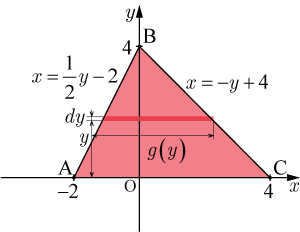置換積分の問題
■問題
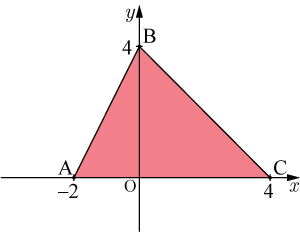
点
,点
,点
を頂点とする三角形の重心の座標を求めよ.
■ヒント
平面の重心の計算より
の公式を用いる.
■解説
三角形の面積
は
・・・・・・(1)
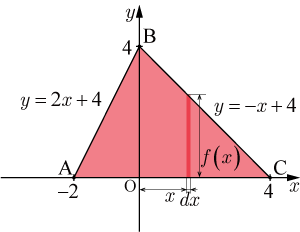
点
,点
を通る直線の方程式は
・・・・・・(2)
点
,点
を通る直線の方程式は
・・・・・・(3)
である.よって
・・・・・・(4)
(2),(3)を
の形に式変形をすると
・・・・・・(5)
・・・・・・(6)
よって
・・・・・・(7)
以上より,重心の座標は
となる.
三角形の重心
を用いると
となり,積分で求めた座標と一致する.
ホーム>>カテゴリー分類>>積分>>積分の問題>>定積分の問題>>区分求積法の問題
最終更新日: 2025年11月2日