重積分の計算問題
■問題
次の重積分の値を求めよ.
■答
■ヒント
領域
の範囲は円になっているので極座標に変数変換する.
■解き方
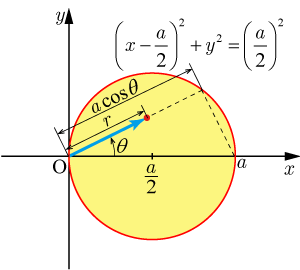
領域
領域の範囲を確認する.
よって,
領域は中心が
,半径が
の内部になる.
極座標変換
,
を行うと,の領域
は図のような
の領域
に移る.
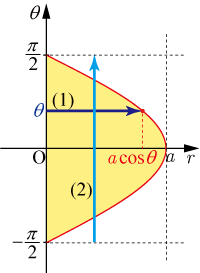
領域
(与式)
について
とおく置換積分をする.
,
,
のとき
よって
したがって
(与式)
は奇関数より, (ここを参照).よって
ホーム>>カテゴリー分類>>積分>>重積分>>重積分の計算問題>>問題
最終更新日:
2023年8月22日

