変数分離形微分方程式
微分方程式
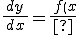%20%20%20%20%5chspace{2}}{%5chspace{2}%20g%20%5c(y%5c)%20%20%20%20%5chspace{2}}%20%20})
を変数分離形という（ただし
%20%20%5cneq%200%20%20})
）．
また
%20%20%20%20%5chspace{2}}{%5chspace{2}%20g%20%5c(y%5c)%20%20%20%20%5chspace{2}}=f%20%5c(x%5c)%20%20%5cfrac{%5chspace{2}1%5chspace{2}}{%5chspace{2}%20g%20%5c(y%5c)%20%20%20%20%5chspace{2}}})
%20%20%20%20%5chspace{2}}=h%20%5c(y%5c)%20%20})
とおくと
%20%20%20%20%5chspace{2}}{%5chspace{2}%20g%20%5c(y%5c)%20%20%20%20%5chspace{2}}=f%20%5c(x%5c)%20%20h%20%5c(y%5c)%20%20})
というように右辺を変形して
%20%20h%20%5c(y%5c)%20%20})
を変数分離形としている場合もある．
■変数分離形微分方程式の解法
その1
%20%20})
%20%20%5cfrac{%5chspace{2}%20dy%20%20%5chspace{2}}{%5chspace{2}%20dx%20%20%5chspace{2}}})
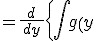%20%20dy%20%20%20%20}%20%20%5c}%20%20%5cfrac{%5chspace{2}%20dy%20%20%5chspace{2}}{%5chspace{2}%20dx%20%20%5chspace{2}}})
%20%20=%5cfrac{%5chspace{2}d%5chspace{2}}{%5chspace{2}%20dy%20%20%5chspace{2}}%20%5c{%20%5cdisplaystyle{%20%5cint%20%20g%20%5c(y%5c)%20%20dy%20%20%20%20}%20%20%5c}%20%20})
(不定積分の定義)
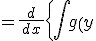%20%20dy%20%20%20%20}%20%20%5c}%20%20})
%20%20dy%20%20%20%20}%20%20})
とおくと，
(合成関数の導関数)
よって，%20%20dy%20%20%20%20}})
が
の原始関数（不定積分）になるので
%20%20dx%20%20%20%20}=%5cdisplaystyle{%20%5cint%20%20g%20%5c(y%5c)%20%20dy%20%20%20%20}+C})
その2
%20%20%5cfrac{%5chspace{2}%20dy%20%20%5chspace{2}}{%5chspace{2}%20dx%20%20%5chspace{2}}=f%20%5c(x%5c)%20%20})
両辺を
で積分する
%20%20%5cfrac{%5chspace{2}%20dy%20%20%5chspace{2}}{%5chspace{2}%20dx%20%20%5chspace{2}}dx%20%20%20%20}=%5cdisplaystyle{%20%5cint%20%20f%20%5c(x%5c)%20%20dx%20%20%20%20}+C})
左辺は置換積分により%20%20%5cfrac{%5chspace{2}%20dy%20%20%5chspace{2}}{%5chspace{2}%20dx%20%20%5chspace{2}}dx%20%20%20%20}=%5cdisplaystyle{%20%5cint%20%20g%20%5c(y%5c)%20%20dy%20%20%20%20}})
となる．
よって
%20%20dy%20%20%20%20}=%5cdisplaystyle{%20%5cint%20%20f%20%5c(x%5c)%20%20dx%20%20%20%20}+C})
その3
形式的に以下のように記述してもよい．
%20%20dy=f%20%5c(x%5c)%20%20dx})
両辺を積分して
%20%20dy=%5cint%20%20f%20%5c(x%5c)%20%20dx%20%20%20%20+C})
ホーム>>カテゴリー分類>>微分>>微分方程式>>変数分離形微分方程式
学生スタッフ作成
最終更新日：
2024年5月17日