ロピタルの定理

関数 $3$\displaystyle{ f\left({x}\right) }$ ， $3$\displaystyle{ g\left({x}\right) }$ が下記に示すi，ii，iiiの条件を満たし， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}=\frac{\hspace{2}0\hspace{2}}{\hspace{2}0\hspace{2}},\frac{\hspace{2}\infty\hspace{2}}{\hspace{2}\infty\hspace{2}} }$ の不定形で， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$ が収束，あるいは， $3$\displaystyle{ \pm \infty }$ のとき

が成り立つ．

$3$\displaystyle{a}$ を含む開区間I( $3$\displaystyle{a}$ を除くことも可能である)で，関数 $3$\displaystyle{ f\left({x}\right) }$ ， $3$\displaystyle{ g\left({x}\right) }$ が微分可能で， $3$\displaystyle{ {g}^{\prime }\left({x}\right)\neq 0 }$ である．
$3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }f\left({x}\right)=0 }$ ， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }g\left({x}\right)=0 }$ ，あるいは， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }f\left({x}\right)=\pm \infty }$ ， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }f\left({x}\right)=\pm \infty }$ である．
$3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$ が存在( $3$\displaystyle{ \pm \infty }$ でもよい)する．

■証明

I． $3$\displaystyle{a}$ を含む開区間Iにおいて，関数 $3$\displaystyle{ f\left({x}\right) }$ ， $3$\displaystyle{ g\left({x}\right) }$ が微分可能， $3$\displaystyle{ {g}^{\prime }\left({x}\right)\neq 0 }$ で， $3$\displaystyle{ f\left({a}\right)=0 }$ ， $3$\displaystyle{ g\left({a}\right)=0 }$ ，かつ， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$ が存在する特殊な場合

$3$\displaystyle{ f\left({a}\right)=0 }$ ， $3$\displaystyle{ g\left({a}\right)=0 }$ より以下のように式を変形することができる．

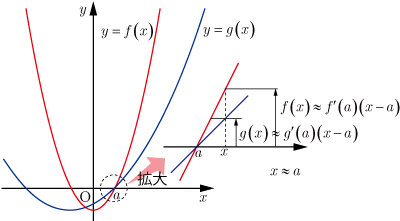$3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}={ \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} f\left({x}\right)- f\left({a}\right) \hspace{2}}{\hspace{2} g\left({x}\right)- g\left({a}\right) \hspace{2}} }$ $3$\displaystyle{ ={ \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} \text{\hspace{5}}\frac{\hspace{2} f\left({x}\right)- f\left({a}\right) \hspace{2}}{\hspace{2} x- a \hspace{2}}\text{\hspace{5}} \hspace{2}}{\hspace{2} \frac{\hspace{2} g\left({x}\right)- g\left({a}\right) \hspace{2}}{\hspace{2} x- a \hspace{2}} \hspace{2}} }$

微分係数の定義式より

$3$\displaystyle{ =\frac{\hspace{2} {f}^{\prime }\left({a}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({a}\right) \hspace{2}} }$

$3$\displaystyle{a}$ を含む開区間Iにおいて，関数 $3$\displaystyle{ f\left({x}\right) }$ ， $3$\displaystyle{ g\left({x}\right) }$ が微分可能より $3$\displaystyle{ {f}^{\prime }\left({x}\right) }$ ， $3$\displaystyle{ {g}^{\prime }\left({x}\right) }$ が連続であることから

$3$\displaystyle{ =\frac{\hspace{2} { \lim }\limits_{ x\rightarrow a }{f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} { \lim }\limits_{ x\rightarrow a }{g}^{\prime }\left({x}\right) \hspace{2}} }$ $3$\displaystyle{ ={ \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$

となる．

II． $3$\displaystyle{a}$ を含む開区間I( $3$\displaystyle{a}$ を除くことも可能である)において，関数 $3$\displaystyle{ f\left({x}\right) }$ ， $3$\displaystyle{ g\left({x}\right) }$ が微分可能， $3$\displaystyle{ {g}^{\prime }\left({x}\right)\neq 0 }$ で， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }f\left({x}\right)=0 }$ ， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }g\left({x}\right)=0 }$ ではあるが $3$\displaystyle{ f\left({a}\right)=0 }$ ， $3$\displaystyle{ g\left({a}\right)=0 }$ とならず，かつ， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$ が存在する特殊な場合

以下に示す関数を導入する．

$3$\displaystyle{ F\left({x}\right)=\left{{ \begin{array}{lll} f\left({x}\right) & x\neq a & \vspace{6}\\ 0& x=a & \vspace{6}\\ \end{array}\text{\hspace{5}} }$ ， $3$\displaystyle{ G\left({x}\right)=\left{{ \begin{array}{lll} g\left({x}\right) & x\neq a & \vspace{6}\\ 0& x=a & \vspace{6}\\ \end{array}\text{\hspace{5}} }$ 　･･････(1)

（ $3$\displaystyle{ F\left({x}\right) }$ ， $3$\displaystyle{ G\left({x}\right) }$ は $3$\displaystyle{ x=a }$ で連続）

証明Iより

$3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} F\left({x}\right) \hspace{2}}{\hspace{2} G\left({x}\right) \hspace{2}}={ \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} {F}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {G}^{\prime }\left({x}\right) \hspace{2}} }$ 　･･････(2)

が成り立つ．

・ $3$\displaystyle{ x> a }$ の場合について

(1)より

$3$\displaystyle{ F\left({x}\right)=f\left({x}\right) }$ ， $3$\displaystyle{ G\left({x}\right)=g\left({x}\right) }$

となり，(2)を(3)のように書き換えることができる.

$3$\displaystyle{ { \lim }\limits_{ x\rightarrow a+0 }\frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}={ \lim }\limits_{ x\rightarrow a+0 }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$ 　･･････(3)

・ $3$\displaystyle{ x< a }$ の場合について

(1)より

$3$\displaystyle{ F\left({x}\right)=f\left({x}\right) }$ ， $3$\displaystyle{ G\left({x}\right)=g\left({x}\right) }$

となり，(2)を(4)のように書き換えることができる.

$3$\displaystyle{ { \lim }\limits_{ x\rightarrow a- 0 }\frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}={ \lim }\limits_{ x\rightarrow a- 0 }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$ 　･･････(4)

(3)と(4)を合わせると

が成り立つ．

III． $3$\displaystyle{a}$ を含む開区間I( $3$\displaystyle{a}$ を除くことも可能である)において，関数 $3$\displaystyle{ f\left({x}\right) }$ ， $3$\displaystyle{ g\left({x}\right) }$ が微分可能， $3$\displaystyle{ {g}^{\prime }\left({x}\right)\neq 0 }$ で， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }f\left({x}\right)=\pm \infty }$ ， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }g\left({x}\right)=\pm \infty }$ ，かつ， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$ が存在する( $3$\displaystyle{ \pm \infty }$ でもよい)場合

$3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}}=\alpha }$ 　･･････(5)

とおく．(5)をε-δ論法で言い換えると

「 $3$\displaystyle{ {\varepsilon}> 0 }$ を任意に1つ選び固定する．この $3$\displaystyle{{\varepsilon}}$ に対して， $3$\displaystyle{ 0< \left|{ x- a }\right|< {\delta}\Rightarrow \left|{ \frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}}- \alpha }\right|< {\varepsilon} }$ を満たすある正の数 $3$\displaystyle{{\delta}}$ が存在する．」　･･････(6)

となる．

・ $3$\displaystyle{ a< x< \hspace{1}{b}_{1} }$ の場合

閉区間 $3$\displaystyle{ \left[{ x,\hspace{1}{b}_{1} }\right] }$ でコーシーの平均値の定理を適用すると

$3$\displaystyle{ \frac{\hspace{2} f\left({x}\right)- f\left({ \hspace{1}{b}_{1} }\right) \hspace{2}}{\hspace{2} g\left({x}\right)- g\left({ \hspace{1}{b}_{1} }\right) \hspace{2}}=\frac{\hspace{2} {f}^{\prime }\left({ \hspace{1}{c}_{1} }\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({ \hspace{1}{c}_{1} }\right) \hspace{2}} }$ 　･･････(7)

を満たす $3$\displaystyle{ \hspace{1}{c}_{1}\text{\hspace{5}}\left({ x< \hspace{1}{c}_{1}< \hspace{1}{b}_{1} }\right) }$ が存在する．

$3$\displaystyle{ \hspace{1}{b}_{1} }$ を $3$\displaystyle{a}$ に近づけていくと， $3$\displaystyle{ \hspace{1}{c}_{1} }$ も $3$\displaystyle{a}$ に近づき， $3$\displaystyle{ 0< \left|{ \hspace{1}{c}_{1}- a }\right|< {\delta} }$ となる．

このとき，(6)より

$3$\displaystyle{ \left|{ \frac{\hspace{2} {f}^{\prime }\left({ \hspace{1}{c}_{1} }\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({ \hspace{1}{c}_{1} }\right) \hspace{2}}- \alpha }\right|< {\varepsilon} }$ 　･･････(8)

が成り立つ．

(7)を以下のように変形する．

$3$\displaystyle{ \frac{\hspace{2} f\left({x}\right)\left{{ 1- \frac{\hspace{2} f\left({ \hspace{1}{b}_{1} }\right) \hspace{2}}{\hspace{2} f\left({x}\right) \hspace{2}} }\right} \hspace{2}}{\hspace{2} g\left({x}\right)\left{{ 1- \frac{\hspace{2} g\left({ \hspace{1}{b}_{1} }\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}} }\right} \hspace{2}}=\frac{\hspace{2} {f}^{\prime }\left({ \hspace{1}{c}_{1} }\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({ \hspace{1}{c}_{1} }\right) \hspace{2}} }$

$3$\displaystyle{ \frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}\cdot \frac{\hspace{2} 1- \frac{\hspace{2} f\left({ \hspace{1}{b}_{1} }\right) \hspace{2}}{\hspace{2} f\left({x}\right) \hspace{2}} \hspace{2}}{\hspace{2} 1- \frac{\hspace{2} g\left({ \hspace{1}{b}_{1} }\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}} \hspace{2}}=\frac{\hspace{2} {f}^{\prime }\left({ \hspace{1}{c}_{1} }\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({ \hspace{1}{c}_{1} }\right) \hspace{2}} }$ 　･･････(9)

(8)に(9)を代入する．

$3$\displaystyle{ \left|{ \frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}\cdot \frac{\hspace{2} 1- \frac{\hspace{2} f\left({ \hspace{1}{b}_{1} }\right) \hspace{2}}{\hspace{2} f\left({x}\right) \hspace{2}} \hspace{2}}{\hspace{2} 1- \frac{\hspace{2} g\left({ \hspace{1}{b}_{1} }\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}} \hspace{2}}- \alpha }\right|< {\varepsilon} }$ 　･･････(10)

$3$\displaystyle{ \hspace{1}{b}_{1} }$ を固定し $3$\displaystyle{ x\rightarrow a+0 }$ の極限をとる．

$3$\displaystyle{ x\rightarrow a+0 }$ のとき， $3$\displaystyle{ f\left({x}\right)\rightarrow \pm \infty }$ ， $3$\displaystyle{ g\left({x}\right)\rightarrow \pm \infty }$ ， $3$\displaystyle{ f\left({ \hspace{1}{b}_{1} }\right) }$ ， $3$\displaystyle{ g\left({ \hspace{1}{b}_{1} }\right) }$ は有限の値なので， $3$\displaystyle{ \frac{\hspace{2} f\left({ \hspace{1}{b}_{1} }\right) \hspace{2}}{\hspace{2} f\left({x}\right) \hspace{2}}\rightarrow 0 }$ ， $3$\displaystyle{ \frac{\hspace{2} g\left({ \hspace{1}{b}_{1} }\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}\rightarrow 0 }$ となり，(10)は

$3$\displaystyle{ \left|{ \frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}- \alpha }\right|< {\varepsilon} }$

となる．よって

$3$\displaystyle{ x\rightarrow a+0 }$ のとき， $3$\displaystyle{ 0< \left|{ \hspace{1}{c}_{1}- a }\right|< {\delta}\Rightarrow \left|{ \frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}- \alpha }\right|< {\varepsilon} }$ 　･･････(11)

が成り立つ．

$3$\displaystyle{a< x< \hspace{1}{c}_{1}< \hspace{1}{b}_{1}}$ より

$3$\displaystyle{0< \left|{ \hspace{1}{c}_{1}- a }\right|< {\delta}\Rightarrow 0< \left|{ x- a }\right|< {\delta}}$

したがって

$3$\displaystyle{x\rightarrow a+0}$ のとき， $3$\displaystyle{0< \left|{ x- a }\right|< {\delta}\Rightarrow \left|{ \frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}- \alpha }\right|< {\varepsilon}}$

すなわち

$3$\displaystyle{ { \lim }\limits_{ x\rightarrow a+0 }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}}=\alpha }$ 　のとき， $3$\displaystyle{{ \lim }\limits_{ x\rightarrow a+0 }\frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}=\alpha }$ 　･･････(12)

成り立つ

・ $3$\displaystyle{ \hspace{1}{b}_{2}< x< a }$ の場合

閉区間 $3$\displaystyle{\left[{ \hspace{1}{b}_{2},x }\right]}$ でコーシーの平均値の定理を適用すると

$3$\displaystyle{ \frac{\hspace{2} f\left({ \hspace{1}{b}_{2} }\right)- f\left({x}\right) \hspace{2}}{\hspace{2} g\left({ \hspace{1}{b}_{2} }\right)- g\left({x}\right) \hspace{2}}=\frac{\hspace{2} {f}^{\prime }\left({ \hspace{1}{c}_{2} }\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({ \hspace{1}{c}_{2} }\right) \hspace{2}} }$ 　･･････(13)

を満たす $3$\displaystyle{ \hspace{1}{c}_{2}\text{\hspace{5}}\left({ x< \hspace{1}{c}_{2}< \hspace{1}{b}_{2} }\right) }$ が存在する．

$3$\displaystyle{ \hspace{1}{b}_{2} }$ を $3$\displaystyle{a}$ に近づけていくと， $3$\displaystyle{ \hspace{1}{c}_{2} }$ も $3$\displaystyle{a}$ に近づき， $3$\displaystyle{ 0< \left|{ \hspace{1}{c}_{2}- a }\right|< {\delta} }$ となる．

このとき，(6)より

$3$\displaystyle{ \left|{ \frac{\hspace{2} {f}^{\prime }\left({ \hspace{1}{c}_{2} }\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({ \hspace{1}{c}_{2} }\right) \hspace{2}}- \alpha }\right|< {\varepsilon} }$ 　･･････(14)

が成り立つ．

(13)を以下のように変形する．

$3$\displaystyle{ \frac{\hspace{2} f\left({x}\right)\left{{ \frac{\hspace{2} f\left({ \hspace{1}{b}_{2} }\right) \hspace{2}}{\hspace{2} f\left({x}\right) \hspace{2}}- 1 }\right} \hspace{2}}{\hspace{2} g\left({x}\right)\left{{ \frac{\hspace{2} g\left({ \hspace{1}{b}_{2} }\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}- 1 }\right} \hspace{2}}=\frac{\hspace{2} {f}^{\prime }\left({ \hspace{1}{c}_{2} }\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({ \hspace{1}{c}_{2} }\right) \hspace{2}} }$

$3$\displaystyle{ \frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}\cdot \frac{\hspace{2} \frac{\hspace{2} f\left({ \hspace{1}{b}_{2} }\right) \hspace{2}}{\hspace{2} f\left({x}\right) \hspace{2}}- 1 \hspace{2}}{\hspace{2} \frac{\hspace{2} g\left({ \hspace{1}{b}_{2} }\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}- 1 \hspace{2}}=\frac{\hspace{2} {f}^{\prime }\left({ \hspace{1}{c}_{2} }\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({ \hspace{1}{c}_{2} }\right) \hspace{2}} }$ 　･･････(15)

(14)に(15)を代入する．

$3$\displaystyle{ \left|{ \frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}\cdot \frac{\hspace{2} \frac{\hspace{2} f\left({ \hspace{1}{b}_{2} }\right) \hspace{2}}{\hspace{2} f\left({x}\right) \hspace{2}}- 1 \hspace{2}}{\hspace{2} \frac{\hspace{2} g\left({ \hspace{1}{b}_{2} }\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}- 1 \hspace{2}}- \alpha }\right|< {\varepsilon} }$ 　･･････(16)

$3$\displaystyle{ \hspace{1}{b}_{2} }$ を固定し $3$\displaystyle{ x\rightarrow a- 0 }$ の極限をとる．

$3$\displaystyle{ x\rightarrow a- 0 }$ のとき， $3$\displaystyle{ f\left({x}\right)\rightarrow \pm \infty }$ ， $3$\displaystyle{ g\left({x}\right)\rightarrow \pm \infty }$ ， $3$\displaystyle{ f\left({ \hspace{1}{b}_{2} }\right) }$ ， $3$\displaystyle{ g\left({ \hspace{1}{b}_{2} }\right) }$ は有限の値なので， $3$\displaystyle{ \frac{\hspace{2} f\left({ \hspace{1}{b}_{2} }\right) \hspace{2}}{\hspace{2} f\left({x}\right) \hspace{2}}\rightarrow 0 }$ ， $3$\displaystyle{ \frac{\hspace{2} g\left({ \hspace{1}{b}_{2} }\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}\rightarrow 0 }$ となり，(16)は

$3$\displaystyle{ \left|{ \frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}- \alpha }\right|< {\varepsilon} }$

となる．よって

$3$\displaystyle{ x\rightarrow a- 0 }$ のとき， $3$\displaystyle{ 0< \left|{ \hspace{1}{c}_{2}- a }\right|< {\delta}\Rightarrow \left|{ \frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}- \alpha }\right|< {\varepsilon} }$ 　･･････(17)

が成り立つ．

$3$\displaystyle{\hspace{1}{b}_{2}< \hspace{1}{c}_{2}< x< a}$ より

$3$\displaystyle{0< \left|{ \hspace{1}{c}_{2}- a }\right|< {\delta}\Rightarrow 0< \left|{ x- a }\right|< {\delta}}$

したがって

$3$\displaystyle{x\rightarrow a- 0}$ のとき， $3$\displaystyle{0< \left|{ x- a }\right|< {\delta}\Rightarrow \left|{ \frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}- \alpha }\right|< {\varepsilon}}$

すなわち

$3$\displaystyle{ { \lim }\limits_{ x\rightarrow a- 0 }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}}=\alpha }$ 　のとき， $3$\displaystyle{{ \lim }\limits_{ x\rightarrow a- 0 }\frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}=\alpha }$ 　･･････(18)

成り立つ

(12)と(18)を合わせると

$3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}}=\alpha }$ のとき， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow a }\frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}=\alpha }$

すなわち

が成り立つ．

IY． $3$\displaystyle{ a\rightarrow \pm \infty }$ の場合

$3$\displaystyle{ t=\frac{\hspace{2}1\hspace{2}}{\hspace{2}x\hspace{2}} }$ となる変数 $3$\displaystyle{t}$ と $3$\displaystyle{ f\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right)=H\left({t}\right) }$ ， $3$\displaystyle{ g\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right)=I\left({t}\right) }$ となる関数 $3$\displaystyle{ H\left({t}\right) }$ ， $3$\displaystyle{ I\left({t}\right) }$ を導入する．

$3$\displaystyle{t\neq 0}$ ， $3$\displaystyle{x\rightarrow \pm \infty}$ のとき $3$\displaystyle{t\rightarrow \pm 0}$ である．

$3$\displaystyle{ {H}^{\prime }\left({t}\right)={ \left{{ f\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right) }\right} }^{\prime } }$ $3$\displaystyle{ ={f}^{\prime }\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right)\times { \left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right) }^{\prime } }$ $3$\displaystyle{ ={f}^{\prime }\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right)\times \left({ - \frac{\hspace{2}1\hspace{2}}{\hspace{2} {t}^{2} \hspace{2}} }\right) }$

$3$\displaystyle{ {I}^{\prime }\left({t}\right)={ \left{{ g\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right) }\right} }^{\prime } }$ $3$\displaystyle{ ={f}^{\prime }\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right)\times { \left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right) }^{\prime } }$ $3$\displaystyle{ ={g}^{\prime }\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right)\times \left({ - \frac{\hspace{2}1\hspace{2}}{\hspace{2} {t}^{2} \hspace{2}} }\right) }$

より

関数 $3$\displaystyle{ H\left({t}\right) }$ ， $3$\displaystyle{ I\left({t}\right) }$ は0を除く0の近傍で微分可能で， $3$\displaystyle{ I\left({t}\right)\neq 0 }$ である．･･････(20)

また

$3$\displaystyle{ { \lim }\limits_{ t\rightarrow \pm 0 }\frac{\hspace{2} {H}^{\prime }\left({t}\right) \hspace{2}}{\hspace{2} {I}^{\prime }\left({t}\right) \hspace{2}}={ \lim }\limits_{ t\rightarrow \pm 0 }\frac{\hspace{2} {f}^{\prime }\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right)\left({ - \frac{\hspace{2}1\hspace{2}}{\hspace{2} {t}^{2} \hspace{2}} }\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right)\left({ - \frac{\hspace{2}1\hspace{2}}{\hspace{2} {t}^{2} \hspace{2}} }\right) \hspace{2}} }$ $3$\displaystyle{ ={ \lim }\limits_{ t\rightarrow \pm 0 }\frac{\hspace{2} {f}^{\prime }\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({ \frac{\hspace{2}1\hspace{2}}{\hspace{2}t\hspace{2}} }\right) \hspace{2}}{ =\lim }\limits_{ x\rightarrow \pm \infty }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$

より

$3$\displaystyle{ { \lim }\limits_{ x\rightarrow \pm \infty }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$ が存在すると $3$\displaystyle{ { \lim }\limits_{ t\rightarrow \pm 0 }\frac{\hspace{2} {H}^{\prime }\left({t}\right) \hspace{2}}{\hspace{2} {I}^{\prime }\left({t}\right) \hspace{2}} }$ も存在する．･･････(21)

・ $3$\displaystyle{ { \lim }\limits_{ x\rightarrow \pm \infty }f\left({x}\right)=0 }$ ， $3$ { \lim }\limits_{ x\rightarrow \pm \infty }g\left({x}\right)=0$ の時

$3$\displaystyle{ x\rightarrow \pm \infty }$ のとき， $3$\displaystyle{ t\rightarrow \pm 0 }$ となることより

$3$\displaystyle{ { \lim }\limits_{ t\rightarrow \pm 0 }H\left({x}\right)=0 }$ ， $3$\displaystyle{ { \lim }\limits_{ t\rightarrow \pm 0 }I\left({x}\right)=0 }$ 　･･････(22)

となる．(20)，(21)，(22)より(3)および(4)が適用でき

$3$\displaystyle{ { \lim }\limits_{ t\rightarrow +0 }\frac{\hspace{2} H\left({t}\right) \hspace{2}}{\hspace{2} I\left({t}\right) \hspace{2}}={ \lim }\limits_{ t\rightarrow +0 }\frac{\hspace{2} {H}^{\prime }\left({t}\right) \hspace{2}}{\hspace{2} {I}^{\prime }\left({t}\right) \hspace{2}} }$

すなわち

$3$\displaystyle{ { \lim }\limits_{ x\rightarrow \pm \infty }\frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}={ \lim }\limits_{ x\rightarrow \pm \infty }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$ 　･･････(23)

が得られる．

・ $3$\displaystyle{ { \lim }\limits_{ x\rightarrow \pm \infty }f\left({x}\right)=\pm \infty }$ ， $3$\displaystyle{ { \lim }\limits_{ x\rightarrow \pm \infty }g\left({x}\right)=\pm \infty }$ の時

$3$\displaystyle{ x\rightarrow \pm \infty }$ のとき， $3$\displaystyle{ t\rightarrow \pm 0 }$ となることより

$3$\displaystyle{ { \lim }\limits_{ t\rightarrow \pm 0 }H\left({x}\right)=\pm \infty }$ ， $3$\displaystyle{ { \lim }\limits_{ t\rightarrow \pm 0 }I\left({x}\right)=\pm \infty }$ 　･･････(24)

となる．(20)，(21)，(24)より(12)，(18)が適用でき

$3$\displaystyle{ { \lim }\limits_{ t\rightarrow \pm 0 }\frac{\hspace{2} H\left({t}\right) \hspace{2}}{\hspace{2} I\left({t}\right) \hspace{2}}={ \lim }\limits_{ t\rightarrow \pm 0 }\frac{\hspace{2} {H}^{\prime }\left({t}\right) \hspace{2}}{\hspace{2} {I}^{\prime }\left({t}\right) \hspace{2}} }$

すなわち

$3$\displaystyle{ { \lim }\limits_{ x\rightarrow \pm \infty }\frac{\hspace{2} f\left({x}\right) \hspace{2}}{\hspace{2} g\left({x}\right) \hspace{2}}={ \lim }\limits_{ x\pm \rightarrow \infty }\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$ 　･･････(25)

が得られる．

【参考図書】
微分積分キャンパスゼミ　著者：高杉豊，馬場敬之　出版社：マセマ出版社
Calculus 7E 著者：James Stewart　出版社：Brooks/Cole Pub Co

ホーム>>カテゴリー分類>>微分>>ロピタルの定理

最終更新日： 2024年5月17日

ロピタルの定理

■証明

I． を含む開区間Iにおいて，関数 ， が微分可能， で， ，，かつ， が存在する特殊な場合

II． を含む開区間I( を除くことも可能である)において，関数 ， が微分可能， で，，ではあるが ，とならず，かつ， が存在する特殊な場合

III． を含む開区間I( を除くことも可能である)において，関数 ， が微分可能， で， ，，かつ， が存在する( でもよい)場合

IY． の場合

IY． $3$\displaystyle{ a\rightarrow \pm \infty }$ の場合