コーシーの平均値定理

2つの関数 $3$\displaystyle{ f\left({x}\right) }$ , $3$\displaystyle{ g\left({x}\right) }$ が閉区間 $3$\displaystyle{ \left[{ a,b }\right] }$ で連続，開区間 $3$\displaystyle{ \left({ a,b }\right) }$ で微分可能であり， $3$\displaystyle{ g\left({x}\right) }$ が開区間 $3$\displaystyle{ \left({ a,b }\right) }$ で $3$\displaystyle{ {g}^{\prime }\left({x}\right)\neq 0 }$ かつ $3$\displaystyle{ g\left({a}\right)\neq g\left({b}\right) }$ であるならば，

$3$\displaystyle{ \frac{\hspace{2} f\left({b}\right)- f\left({a}\right) \hspace{2}}{\hspace{2} g\left({b}\right)- g\left({a}\right) \hspace{2}}=\frac{\hspace{2} {f}^{\prime }\left({c}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({c}\right) \hspace{2}} }$ 　　 $3$\displaystyle{ \left({ a< c< b }\right) }$

を満たす $3$\displaystyle{c}$ が少なくとも１つ存在する.

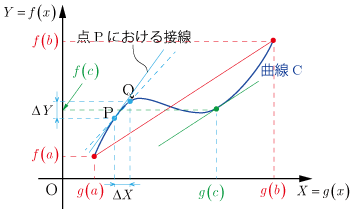
■証明

$3$\displaystyle{ X=g\left({x}\right) }$ ， $3$\displaystyle{ Y=f\left({x}\right) }$ とおく．

媒介変数 $3$\displaystyle{x}$ で表される曲線 $3$\displaystyle{C}$

$3$\displaystyle{ \left{{\begin{array}{lll}X=g\left({x}\right)& \vspace{6}\\ Y=f\left({x}\right)& \vspace{6}\\ \end{array}\text{\hspace{5}}\left({ a\leq x\leq b }\right) }$

を考える．

$3$\displaystyle{ g\left({x}\right) }$ が開区間 $3$\displaystyle{ \left({ a,b }\right) }$ で $3$\displaystyle{ \left({ a,b }\right) }$ かつ $3$\displaystyle{ g\left({a}\right)\neq g\left({b}\right) }$ であることより，開区間 $3$\displaystyle{ \left({ a,b }\right) }$ で $3$\displaystyle{ X=g\left({x}\right) }$ は単調増加あるいは単調減少する．よって， $3$\displaystyle{X}$ を $3$\displaystyle{Y}$ に対応させる関数 $3$\displaystyle{ Y=F\left({X}\right) }$ が存在する．すなわち，曲線 $3$\displaystyle{ Y=F\left({X}\right) }$ の式は $3$\displaystyle{ Y=F\left({X}\right) }$ と表すこともできる．

点Pの座標を $3$\displaystyle{ \left({ g\left({x}\right),f\left({x}\right) }\right) }$ ，点Qの座標を $3$\displaystyle{ \left({ g\left({ x+{\Delta}x }\right),f\left({ x+{\Delta}y }\right) }\right) }$ とする．

$3$\displaystyle{ {\Delta}x\rightarrow 0 }$ のとき，点Pと点Qを通る直線は点Pを通る曲線 $3$\displaystyle{C}$ の接線に限りなく近づく．

$3$\displaystyle{ \left{{\begin{array}{lll}{\Delta}X=g\left({ x+{\Delta}x }\right)- g\left({x}\right)& \vspace{6}\\ {\Delta}Y=f\left({ x+{\Delta}x }\right)- f\left({x}\right)& \vspace{6}\\ \end{array} }$

とすると，点Pと点Qを通る直線の傾き $3$\displaystyle{m}$ は

$3$\displaystyle{ m={F}^{\prime }\left({X}\right)={ \lim }\limits_{ {\Delta}X\rightarrow 0 }\frac{\hspace{2} {\Delta}Y \hspace{2}}{\hspace{2} {\Delta}X \hspace{2}} }$

$3$\displaystyle{ ={ \lim }\limits_{ {\Delta}x\rightarrow 0 }\frac{\hspace{2} f\left({ x+{\Delta}x }\right)- f\left({x}\right) \hspace{2}}{\hspace{2} g\left({ x+{\Delta}x }\right)- g\left({x}\right) \hspace{2}} }$

$3$\displaystyle{ ={ \lim }\limits_{ {\Delta}x\rightarrow 0 }\frac{\hspace{2} \text{\hspace{5}}\frac{\hspace{2} f\left({ x+{\Delta}x }\right)- f\left({x}\right) \hspace{2}}{\hspace{2} {\Delta}x \hspace{2}}\text{\hspace{5}} \hspace{2}}{\hspace{2} \frac{\hspace{2} g\left({ x+{\Delta}x }\right)- g\left({x}\right) \hspace{2}}{\hspace{2} {\Delta}x \hspace{2}} \hspace{2}} }$

$3$\displaystyle{ =\frac{\hspace{2} \text{\hspace{5}}{ \lim }\limits_{ {\Delta}x\rightarrow 0 }\frac{\hspace{2} f\left({ x+{\Delta}x }\right)- f\left({x}\right) \hspace{2}}{\hspace{2} {\Delta}x \hspace{2}}\text{\hspace{5}} \hspace{2}}{\hspace{2} { \lim }\limits_{ {\Delta}x\rightarrow 0 }\frac{\hspace{2} g\left({ x+{\Delta}x }\right)- g\left({x}\right) \hspace{2}}{\hspace{2} {\Delta}x \hspace{2}} \hspace{2}} }$

関数 $3$\displaystyle{ f\left({x}\right) }$ , $3$\displaystyle{ g\left({x}\right) }$ が閉区間 $3$\displaystyle{ \left[{ a,b }\right] }$ で連続，開区間 $3$\displaystyle{ \left({ a,b }\right) }$ で微分可能であることと， $3$\displaystyle{ g\left({x}\right) }$ が開区間 $3$\displaystyle{ \left({ a,b }\right) }$ で $3$\displaystyle{ {g}^{\prime }\left({x}\right)\neq 0 }$ より

$3$\displaystyle{ =\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}} }$

となる．すなわち，

$3$\displaystyle{ {F}^{\prime }\left({X}\right)=\frac{\hspace{2} {f}^{\prime }\left({x}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({x}\right) \hspace{2}}\text{\hspace{5}}\left({ X=g\left({x}\right) }\right) }$ 　･････(1)

となる．

$3$\displaystyle{ \alpha =g\left({a}\right) }$ ， $3$ {\beta}=g\left({b}\right)$ とおくと， $3$\displaystyle{ f\left({a}\right)=F\left({\alpha }\right) }$ ， $3$ f\left({b}\right)=F\left({{\beta}}\right)$ となり

$3$\displaystyle{ \frac{\hspace{2} f\left({b}\right)- f\left({a}\right) \hspace{2}}{\hspace{2} g\left({b}\right)- g\left({a}\right) \hspace{2}}=\frac{\hspace{2} F\left({{\beta}}\right)- F\left({\alpha }\right) \hspace{2}}{\hspace{2} {\beta}- \alpha \hspace{2}} }$ 　･････(2)

と書き換えることができる．

中間値の定理より，

$3$\displaystyle{ \frac{\hspace{2} F\left({{\beta}}\right)- F\left({\alpha }\right) \hspace{2}}{\hspace{2} {\beta}- \alpha \hspace{2}}={F}^{\prime }\left({{\gamma}}\right) }$ となる $3$\displaystyle{ {\gamma}\text{\hspace{5}}\left({ \alpha < {\gamma}< {\beta} }\right) }$ が少なくとも１つ存在する．･････(3)

$3$\displaystyle{ X=g\left({x}\right) }$ より

$3$\displaystyle{ {\gamma}=g\left({c}\right)\text{\hspace{5}}\left({ a< c< b }\right) }$ 　･････(4)

と表すことができる．

(1)と(4)より

$3$\displaystyle{ {F}^{\prime }\left({{\gamma}}\right)=\frac{\hspace{2} {f}^{\prime }\left({c}\right) \hspace{2}}{\hspace{2} {g}^{\prime }\left({c}\right) \hspace{2}} }$ 　･････(5)

となる．(2)，(3)，(5)より

を満たす $3$\displaystyle{c}$ が少なくとも１つ存在する.

【参考図書】
微分積分キャンパスゼミ　著者：高杉豊，馬場敬之　出版社：マセマ出版社
Calculus 7E 著者：James Stewart　出版社：Brooks/Cole Pub Co

ホーム>>カテゴリー分類>>微分>>平均値の定理

最終更新日： 2024年5月17日