成分が複素数の場合の内積(n次元ベクトル)
ベクトルの成分を実数から複素数に拡張した場合,内積の定義は以下のようになる.(参考:成分が実数の場合の内積)
 次元列ベクトル
次元列ベクトル
}) ,
,}) (
( ,
, は複素数)
は複素数)
において

となる値を, ,
, の内積と定義し
の内積と定義し

で表す.すなわち
 ・・・・・・(1)
・・・・・・(1)
となる.内積を行列の計算表現を使うと
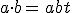
%5cleft({%20%5cbegin{array}%20%5cbar{%20%5chspace{1}{b}_{1}%20%20}%20%20&%20%5cvspace{6}%5c%5c%20%20%5cbar{%20%5chspace{1}{b}_{2}%20%20}%20%20&%20%5cvspace{6}%5c%5c%20%5cvdots%20&%20%5cvspace{6}%5c%5c%20%20%5cbar{%20%5chspace{1}{b}_{n}%20%20}%20%20&%20%5cvspace{6}%5c%5c%20%20%5cend{array}%20%20}%5cright)%20%20})
となる.
行ベクトルでも列ベクトルと同様に内積は(1)で定義される.
内積については次の法則が成り立つ.
(i) 
(∵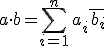
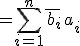
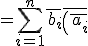%20%20}%20%20}})
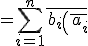%20%20}%20%20}})
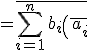%20%20}%20%20}})
 )
)
(ii) %5ccdot%20%5cdisplaystyle{c}=%5cdisplaystyle{a}%5ccdot%20%5cdisplaystyle{c}+%5cdisplaystyle{b}%5ccdot%20%5cdisplaystyle{c}})
(iii) %5ccdot%20%5cdisplaystyle{b}=%5cdisplaystyle{a}%5ccdot%20%5cleft({%20%5cbar{k}%5cdisplaystyle{b}%20%20}%5cright)=k%5cleft({%20%5cdisplaystyle{a}%5ccdot%20%5cdisplaystyle{b}%20%20}%5cright)})
(∵%5ccdot%20%5cdisplaystyle{b}=%5cdisplaystyle{{%5csum%20}%5climits_{%20i=1%20%20}^{n}%20%5cleft({%20k%5chspace{1}{a}_{i}%20%20}%5cright)%5cbar{%20%5chspace{1}{b}_{i}%20%20}%20%20}%5ctext{%5chspace{1}}})
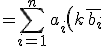%20%20}})
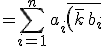%20%20}%20%20}})
})
%5ccdot%20%5cdisplaystyle{b}=%5cdisplaystyle{{%5csum%20}%5climits_{%20i=1%20%20}^{n}%20%5cleft({%20k%5chspace{1}{a}_{i}%20%20}%5cright)%5cbar{%20%5chspace{1}{b}_{i}%20%20}%20%20}})
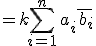
}) )
)
(iv)  ,特に,
,特に,
ホーム>>カテゴリー分類>>行列>>線形代数>>成分が複素数の場合の内積
最終更新日:2022年9月3日