| ||||||||||||
|
線形写像の合成
2つの線形写像
,
がある.
は
次元ベクトル空間,
は
次元ベクトル空間,
は
次元ベクトル空間である.
の要素
は
により
の要素
に対応し,
の要素
は
により
の要素
に対応する.
と
の線形写像を続けて行うことにより,
の要素
は
の要素
に対応する.
このように2つの写像を連続して行う対応を写像の合成といい,合成された写像(合成写像)をとすると
で表す.合成写像の概念を図で表すと下図のようになる.
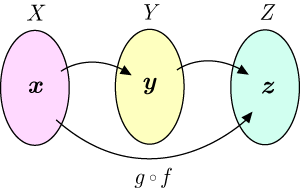
線形写像
の表現行列を
,線形写像
の表現行列を
とすると,
合成された写像も線形写像となり,その表現行列は
となる.
■導出
・・・・・・(1)
・・・・・・(2)
(2)に(1)を代入すると,言い換えると,写像を合成すると,
(∵行列の計算則)
すなわち
となる.
を使って表すと
となる.よって,合成された写像も線形写像となり,その表現行列は
となる.(
でないことに注意
)
ホーム>>カテゴリー分類>>行列>>線形代数>>線形写像の合成
最終更新日: 2025年1月20日