離心率

$3$\displaystyle{0\leq ε< 1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
：楕円
$3$\displaystyle{ε=1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
：放物線
$3$\displaystyle{ε> 1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
：双曲線

JSXGraph Copyright (C) see http://jsxgraph.org

平面における点 $3$\displaystyle{\text{P}}$ について，定点 $3$\displaystyle{\text{F}}$ までの距離を $3$\displaystyle{\text{PF}}$ ，点 $3$\displaystyle{\text{F}}$ を通らない直線 $3$\displaystyle{\text{L}}$ までの距離を $3$\displaystyle{\text{PH}}$ とする（ $3$\displaystyle{\text{H}}$ は点 $3$\displaystyle{\text{P}}$ から直線 $3$\displaystyle{\text{L}}$ におろした垂線との交点）．このとき， $3$\displaystyle{\text{PF}}$ と $3$\displaystyle{\text{PH}}$ との比が一定である点 $3$\displaystyle{\text{P}}$ の軌跡は2次曲線を表し，その比を離心率という．

離心率 $3$\displaystyle{ {\varepsilon}=\frac{\hspace{2} \text{PF} \hspace{2}}{\hspace{2} \text{PH} \hspace{2}} }$ ······ (1)

また， $3$\displaystyle{\text{F}}$ を焦点， $3$\displaystyle{\text{L}}$ を準線という．離心率 $3$\displaystyle{ε}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
により，2次曲線は以下のように分類される．

楕円 $3$\displaystyle{\Leftrightarrow }$ $3$\displaystyle{0\leq ε< 1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
（ $3$\displaystyle{ε=0}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
のときに円となる）
放物線 $3$\displaystyle{\Leftrightarrow }$ $3$\displaystyle{ε=1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
双曲線 $3$\displaystyle{\Leftrightarrow }$ $3$\displaystyle{ε> 1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。

$3$\displaystyle{ε\neq 1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
について，軌道長半径を $3$\displaystyle{α}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
，軌道短半径を $3$\displaystyle{β}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
$3$\displaystyle{$\leq α$}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
とすると

楕円 ( $3$\displaystyle{0\leq ε< 1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
) の離心率： $3$\displaystyle{ε=\frac{\hspace{2} \sqrt{{α}^{2}- {β}^{2}} \hspace{2}}{\hspace{2}α\hspace{2}}}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
······ (2)

双曲線 ( $3$\displaystyle{ε> 1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
) の離心率： $3$\displaystyle{ε=\frac{\hspace{2} \sqrt{{α}^{2}+{β}^{2}} \hspace{2}}{\hspace{2}α\hspace{2}}}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
······ (3)

である．

■ 2次曲線の式の導出

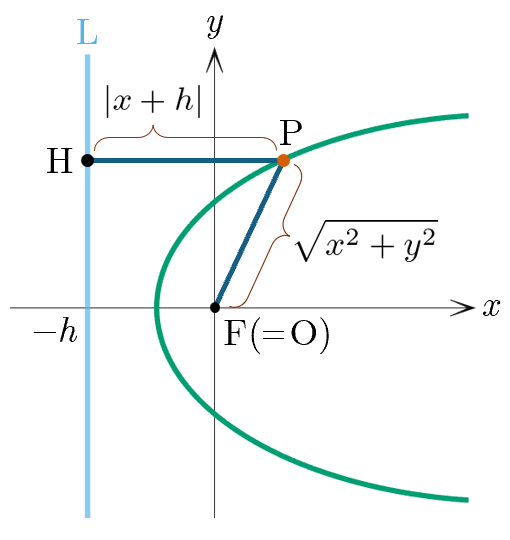
焦点 $3$\displaystyle{\text{F}}$ を原点 $3$\displaystyle{\text{O}}$ にとり，点 $3$\displaystyle{\text{P}}$ の座標を $3$\displaystyle{$x,y$}$ とし，直線 $3$\displaystyle{x=- h}$ を準線 $3$\displaystyle{\text{L}}$ とする（ $3$\displaystyle{h> 0}$ ）．このとき，距離 $3$\displaystyle{\text{PF}=\sqrt{{x}^{2}+{y}^{2}}}$ ，距離 $3$\displaystyle{\text{PH}=\|x+h\|}$ であるので，離心率 $3$\displaystyle{ε}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
は

$3$\displaystyle{ {\varepsilon}=\frac{\hspace{2} \text{PF} \hspace{2}}{\hspace{2} \text{PH} \hspace{2}} }$ $3$\displaystyle{ =\frac{\hspace{2} \sqrt{{x}^{2}+{y}^{2}} \hspace{2}}{\hspace{2} \|x+h\| \hspace{2}} }$ ······ (4)

と表せる．したがって，上式を整理すると

$3$\displaystyle{ {\varepsilon}\|x+h\|=\sqrt{{x}^{2}+{y}^{2}} }$

$3$\displaystyle{\Leftrightarrow }$ $3$\displaystyle{ {{\varepsilon}}^{2}{ $x+h$ }^{2}={x}^{2}+{y}^{2} }$

$3$\displaystyle{\Leftrightarrow }$ $3$\displaystyle{ $1- {{\varepsilon}}^{2}${x}^{2}+{y}^{2}- 2h{{\varepsilon}}^{2}x- {h}^{2}{{\varepsilon}}^{2}=0 }$ ······ (5)

となり，2次曲線の式が得られる．

楕円の場合 ( $3$\displaystyle{0\leq ε< 1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
)

式(5)より

$3$\displaystyle{ $1- {{\varepsilon}}^{2}${ $x- \frac{\hspace{2} h{{\varepsilon}}^{2} \hspace{2}}{\hspace{2} 1- {{\varepsilon}}^{2} \hspace{2}}$ }^{2}+{y}^{2}- \frac{\hspace{2} {h}^{2}{{\varepsilon}}^{2} \hspace{2}}{\hspace{2} 1- {{\varepsilon}}^{2} \hspace{2}}=0 }$

$3$\displaystyle{\Leftrightarrow }$ $3$\displaystyle{ \frac{\hspace{2} { $x- \frac{\hspace{2} h{{\varepsilon}}^{2} \hspace{2}}{\hspace{2} 1- {{\varepsilon}}^{2} \hspace{2}}$ }^{2} \hspace{2}}{\hspace{2}{ $\frac{\hspace{2} h{\varepsilon} \hspace{2}}{\hspace{2} 1- {{\varepsilon}}^{2} \hspace{2}}$ }^{2}\hspace{2}}+\frac{\hspace{2} {y}^{2} \hspace{2}}{\hspace{2}{ $\frac{\hspace{2} h{\varepsilon} \hspace{2}}{\hspace{2}\sqrt{1- {{\varepsilon}}^{2}}\hspace{2}}$ }^{2}\hspace{2}}=1 }$ ······ (6)

のように中心 $3$\displaystyle{$\frac{\hspace{2} h{{\varepsilon}}^{2} \hspace{2}}{\hspace{2} 1- {{\varepsilon}}^{2} \hspace{2}},0$}$ の楕円の方程式として表せるので，軌道長半径 $3$\displaystyle{α}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
と軌道短半径 $3$\displaystyle{β}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
は

$3$\displaystyle{ α=\frac{\hspace{2} h{\varepsilon} \hspace{2}}{\hspace{2} 1- {{\varepsilon}}^{2} \hspace{2}} }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
, $3$\displaystyle{ β=\frac{\hspace{2} h{\varepsilon} \hspace{2}}{\hspace{2}\sqrt{1- {{\varepsilon}}^{2}}\hspace{2}} }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
······ (7)

となる．上の2式から $3$\displaystyle{h}$ を消去すると

$3$\displaystyle{ \frac{\hspace{2}β\hspace{2}}{\hspace{2}α\hspace{2}}=\sqrt{1- {{\varepsilon}}^{2}} }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
$3$\displaystyle{\Leftrightarrow }$ $3$\displaystyle{ε=\frac{\hspace{2} \sqrt{{α}^{2}- {β}^{2}} \hspace{2}}{\hspace{2}α\hspace{2}}}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。

となり，式(2)を得る．

放物線の場合 ( $3$\displaystyle{ε=1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
)

式(5)より

$3$\displaystyle{ {y}^{2}=2h$x+\frac{\hspace{2}h\hspace{2}}{\hspace{2}2\hspace{2}}$ }$ ······ (8)

のように頂点 $3$\displaystyle{$- h/2,0$}$ の放物線として表せる．

双曲線の場合 ( $3$\displaystyle{ε> 1}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
)

式(5)より

$3$\displaystyle{ ${{\varepsilon}}^{2}- 1${ $x+\frac{\hspace{2} h{{\varepsilon}}^{2} \hspace{2}}{\hspace{2} {{\varepsilon}}^{2}- 1 \hspace{2}}$ }^{2}- {y}^{2}- \frac{\hspace{2} {h}^{2}{{\varepsilon}}^{2} \hspace{2}}{\hspace{2} {{\varepsilon}}^{2}- 1 \hspace{2}}=0 }$

$3$\displaystyle{\Leftrightarrow }$ $3$\displaystyle{ \frac{\hspace{2} { $x+\frac{\hspace{2} h{{\varepsilon}}^{2} \hspace{2}}{\hspace{2} {{\varepsilon}}^{2}- 1 \hspace{2}}$ }^{2} \hspace{2}}{\hspace{2}{ $\frac{\hspace{2} h{\varepsilon} \hspace{2}}{\hspace{2} {{\varepsilon}}^{2}- 1 \hspace{2}}$ }^{2}\hspace{2}}- \frac{\hspace{2} {y}^{2} \hspace{2}}{\hspace{2}{ $\frac{\hspace{2} h{\varepsilon} \hspace{2}}{\hspace{2}\sqrt{{{\varepsilon}}^{2}- 1}\hspace{2}}$ }^{2}\hspace{2}}=1 }$ ······ (9)

のように中心 $3$\displaystyle{$- \frac{\hspace{2} h{{\varepsilon}}^{2} \hspace{2}}{\hspace{2} {{\varepsilon}}^{2}- 1 \hspace{2}},0$}$ の双曲線の方程式として表せるので，軌道長半径 $3$\displaystyle{α}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
と軌道短半径 $3$\displaystyle{β}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
は

$3$\displaystyle{ α=\frac{\hspace{2} h{\varepsilon} \hspace{2}}{\hspace{2} {{\varepsilon}}^{2}- 1 \hspace{2}} }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
, $3$\displaystyle{ β=\frac{\hspace{2} h{\varepsilon} \hspace{2}}{\hspace{2}\sqrt{{{\varepsilon}}^{2}- 1}\hspace{2}} }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
······ (10)

となる．上の2式から $3$\displaystyle{h}$ を消去すると

$3$\displaystyle{ \frac{\hspace{2}β\hspace{2}}{\hspace{2}α\hspace{2}}=\sqrt{{{\varepsilon}}^{2}- 1} }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
$3$\displaystyle{\Leftrightarrow }$ $3$\displaystyle{ε=\frac{\hspace{2} \sqrt{{α}^{2}+{β}^{2}} \hspace{2}}{\hspace{2}α\hspace{2}}}$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。

となり，式(3)を得る．

ホーム>>カテゴリー分類>>幾何>>平面幾何>>離心率

最終更新日：2025年10月24日